P13616 [ICPC 2024 APC] Attraction Score

在虚构的国家 Manteiv，有 $n$ 个城市，编号从 $1$ 到 $n$。我们可以将这些城市视为在一个二维坐标系的平面上，其中城市 $i$ 的坐标为 $(x_i, y_i)$。没有两个城市位于相同的位置。 这里有 $m$ 条高速公路，编号从 $1$ 到 $m$，每条高速公路都是以两个不同的城市为其端点的线段，并且沿线设有一定数量的景点。具体来说，高速公路 $j$ 有 $a_j$ 个景点，并连接城市 $u_j$ 和 $v_j$ 作为其端点。由于高速公路上的交叉路口会导致交通堵塞，且在另一条高速公路上方建造新的高速公路成本高昂，因此题目保证： * 任意两条高速公路除了在城市作为端点外，不会在任何其他点相交。 * 任意一条高速公路除了其两个端点城市外，不会穿过任何其他城市。 * 每对城市之间最多只有一条高速公路相连。 Manteiv 旅游部希望选择一个城市子集作为旅游景点。直观地说，旅游部希望所选城市中有许多对城市由景点众多的高速公路相连。形式上，一个非空城市子集 $S$ 的吸引力分数定义如下： * 对于每一对整数 $(a, b)$，如果 $a < b$，城市 $a$ 和城市 $b$ 都在 $S$ 中，并且它们之间有高速公路相连，则将该高速公路的景点数加到分数中。 * 令 $f(S)$ 为满足 $a < b$ 的整数对 $(a, b)$ 的数量，其中城市 $a$ 和城市 $b$ 都在 $S$ 中，但它们之间没有高速公路相连。分数会产生一个惩罚（负）分数，大小为 $10^6$ 乘以 $f(S)$ 的平方。换句话说，从分数中减去 $10^6 \times f(S)^2$。 例如，假设 $n=3$，城市 $1$ 和 $2$ 由一条有 $10$ 个景点的高速公路连接，城市 $2$ 和 $3$ 由一条有 $20$ 个景点的高速公路连接，而城市 $1$ 和 $3$ 之间没有高速公路。 - 城市子集 $\{1\}$ 的吸引力分数为 $0$。 - 城市子集 $\{1,2\}$ 的吸引力分数为 $10 - 10^6 \times 0^2 = 10$。 - 城市子集 $\{2,3\}$ 的吸引力分数为 $20 - 10^6 \times 0^2 = 20$。 - 城市子集 $\{1,2,3\}$ 的吸引力分数为 $10 + 20 - 10^6 \times 1^2 = -999970$。 作为旅游部的顾问，您需要找到所有可能的非空城市子集 $S$ 中最大的吸引力分数。

输入的第一行包含两个整数 $n$ 和 $m$ ($1 \le n \le 100,000; 0 \le m \le 300,000$)。 接下来的 $n$ 行，每行包含两个整数。第 $i$ 行包含 $x_i$ 和 $y_i$ $(0 \le x_i, y_i \le 10^9)$。 再接下来的 $m$ 行，每行包含三个整数。第 $j$ 行包含 $u_j$，$v_j$ 和 $a_j$ $(1 \le u_j < v_j \le n; 0 \le a_j \le 10^6)$。 保证所有高速公路都满足题目描述中的条件。

输出一个整数，代表所有可能的非空城市子集 $S$ 中最大的吸引力分数。

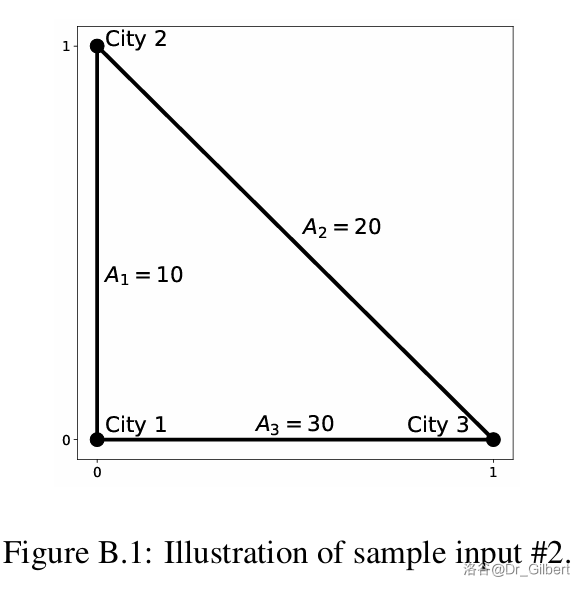
**样例解释 #1** 该样例即为题目描述中给出的例子。城市子集 $\{2,3\}$ 得到了最高的吸引力分数 $20$。 **样例解释 #2** 城市和高速公路如图 B.1 所示。通过在 $S$ 中选择城市 $1, 2, 3$，吸引力分数为 $10 + 20 + 30 - 10^6 \times 0^2 = 60$。