P13623 [ICPC 2024 APC] Symmetric Boundary

对称图形是美丽的，它们也是本题的主题。一个二维平面区域是**凸的**，当且仅当对于区域内的任意一对点 $p$ 和 $q$，连接 $p$ 和 $q$ 的线段完全包含在该区域内。此外，一个二维平面区域是**点对称的**，当且仅当将该区域围绕某个特定点旋转 $180$ 度后，旋转后的区域与原始区域完全重合。 给定一个二维平面上的凸多边形，它有 $n$ 个顶点，按逆时针顺序从 $1$ 到 $n$ 编号。顶点 $i$ 的坐标为 $(x_i, y_i)$。没有三个顶点共线。 请判断是否存在一个凸形的、点对称的区域，其边界包含了所有这 $n$ 个顶点。如果存在一个或多个这样的区域，请计算其中面积最小的区域的面积。

输入的第一行包含一个整数 $n$ ($3 \le n \le 30$)。 接下来的 $n$ 行，每行包含两个整数。第 $i$ 行包含 $x_i$ 和 $y_i$ ($0 \le x_i, y_i \le 1000$)。 保证给定的多边形是凸的，其顶点按逆时针顺序给出，并且没有三个顶点共线。

如果存在一个或多个这样的区域，输出其中的最小面积。输出的相对误差必须在 $10^{-9}$ 以内。 如果不存在这样的区域，则输出 $-1$。

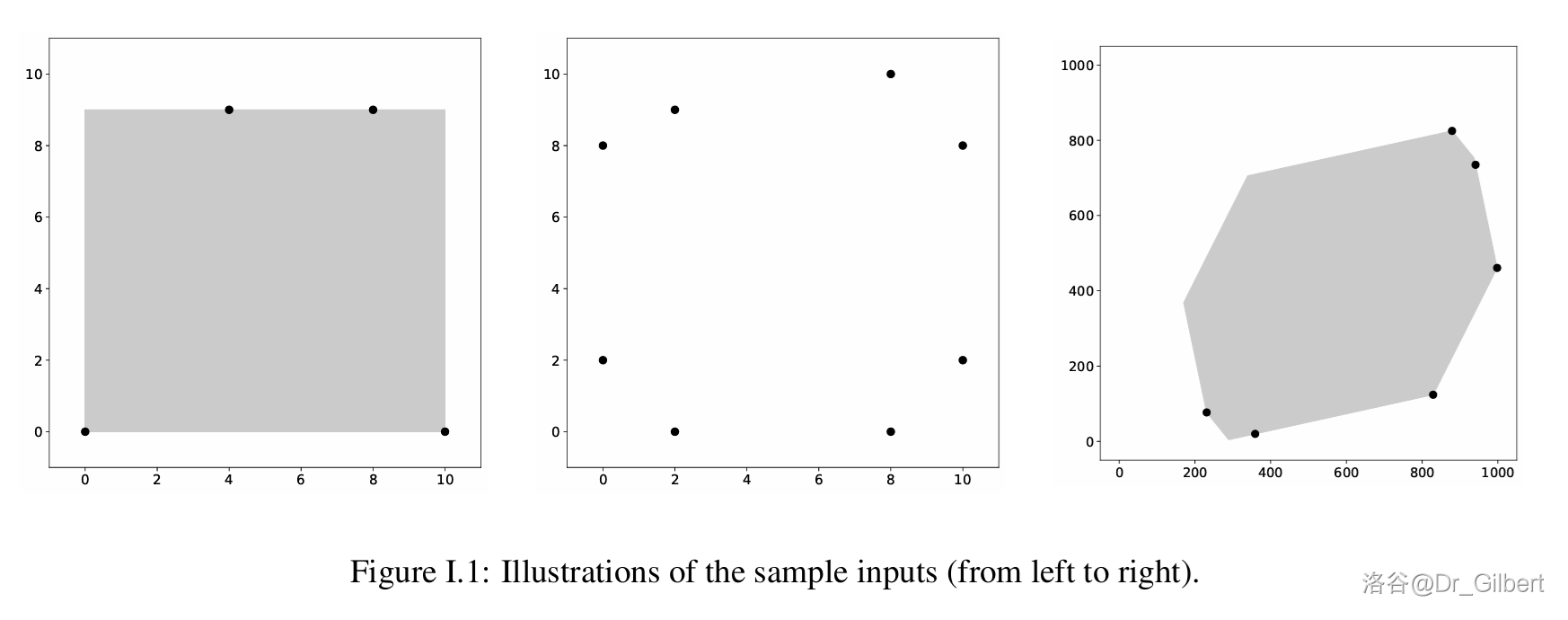
**样例解释** 图 I.1 将样例输入中的顶点以黑点的形式展示了出来。对于样例输入 #1 和 #3，阴影部分代表了可能实现的最小面积区域。