P1364 Hospital Placement

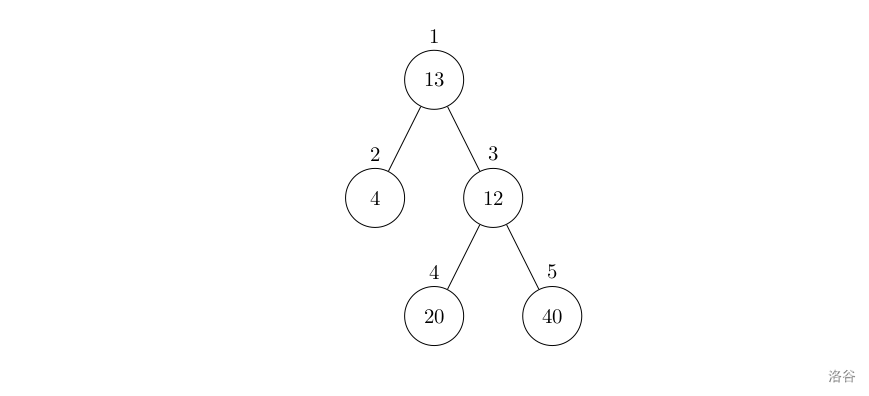
Given a binary tree as shown:  The number inside each circle is the population at that node. The number beside each circle is the node index. Choose one node to build a hospital so that the total distance traveled by all residents is minimized. The distance between two adjacent nodes is $1$. For example, if the hospital is built at node $1$, the total distance is $4 + 12 + 2 \times 20 + 2 \times 40 = 136$. If it is built at node $3$, the total distance is $4 \times 2 + 13 + 20 + 40 = 81$.

The first line contains an integer $n$, the number of nodes in the tree. Each of the next $n$ lines describes one node with three integers $w, u, v$, where $w$ is the population at the node, $u$ is the left child (with $0$ meaning no child), and $v$ is the right child (with $0$ meaning no child).

Output a single integer, the minimum total distance.

Constraints For 100% of the testdata, it is guaranteed that $1 \leq n \leq 100$, $0 \leq u, v \leq n$, $1 \leq w \leq 10^5$. Translated by ChatGPT 5