P13655 [CERC 2020] Tobacco Growing

在城市中，有一个美丽的公园，公园里鲜花盛开。这个公园深受市民喜爱，尤其是有孩子的家庭常常来这里游玩。黑帮分子想要将他们的犯罪活动扩展到这个区域，主要是进行烟草种植。他们决定在公园里偷偷种下烟草种子，让烟草在警察的眼皮底下悄悄生长。当时机成熟时，他们计划在一次行动中尽可能多地收获烟草，并将其走私出境。 公园由若干花坛组成，每个花坛的坐标范围在 $-10^6$ 到 $10^6$ 之间。位于 $(X, Y)$ 的花坛与 $(X + 1, Y)$、$(X - 1, Y)$、$(X, Y + 1)$ 和 $(X, Y - 1)$ 这四个相邻坐标的花坛相邻（前提是这些坐标在范围内）。在第一天，黑帮可以选择任意若干花坛进行割花。并且也只有在第一天，如果一个花坛被割花，黑帮可以选择在该花坛上种植烟草，或者让该花坛只长草。最初，种有烟草的花坛烟草数量为 $1$，而只长草或仍有鲜花的花坛烟草数量为 $0$。当地烟草生长非常迅速，因此在接下来的每一天，公园中各花坛的烟草数量按如下方式增长： - 对于种有烟草和草地的花坛，其烟草数量会增加为前一天相邻花坛的烟草数量之和。 - 对于仍有鲜花的花坛，其烟草数量始终为 $0$。 经过若干天的生长后，黑帮将在某一天进行收割。他们可以选择若干花坛（类型不限）进行收割，并获得这些花坛当天的烟草总量。每个花坛最多只能被收割一次，且被选中的花坛上的所有烟草都必须被收割。黑帮不能把所有烟草都收割走，因为能安全走私的烟草数量有限。同时，黑帮也不想有任何不必要的损失，因此他们希望收割的烟草数量恰好等于这个上限。 你的任务是帮助黑帮精确地制定行动计划。具体来说： 1. 在第一天，选择要割花的花坛，并从中选择要种植烟草的花坛。最多只能割 $2 \times 10^5$ 个花坛，以免引起警察怀疑。 2. 选择烟草生长的天数。天数最多不能超过 $100$，以免烟草生意过于明显。 3. 选择在指定天数后要收割的花坛。最多只能收割 $10^4$ 个花坛，否则收割时间太长。 你能帮助黑帮完成计划吗？祝你好运！

输入包含一行一个整数 $N$（$0 \leq N \leq 10^{18}$），表示需要恰好收割的烟草总量。

第一行输出被割花的花坛数量 $C$（$0 \leq C \leq 2 \times 10^5$）。对于每个被割花的花坛，输出一行，格式为 $X\ Y\ 1$，表示在整数坐标 $(X, Y)$ 的花坛被割花并种植了烟草，或 $X\ Y\ 0$，表示该花坛被割花后只长草（$-10^6 \leq X, Y \leq 10^6$）。 接下来输出一行，包含两个用空格分隔的整数 $H$ 和 $D$（$0 \leq H \leq 10^4$，$0 \leq D \leq 100$），分别表示收割的花坛数量和烟草生长的天数。之后输出 $H$ 行，每行两个用空格分隔的整数 $X$ 和 $Y$（$-10^6 \leq X, Y \leq 10^6$），表示在第 $D$ 天后要收割的花坛坐标。

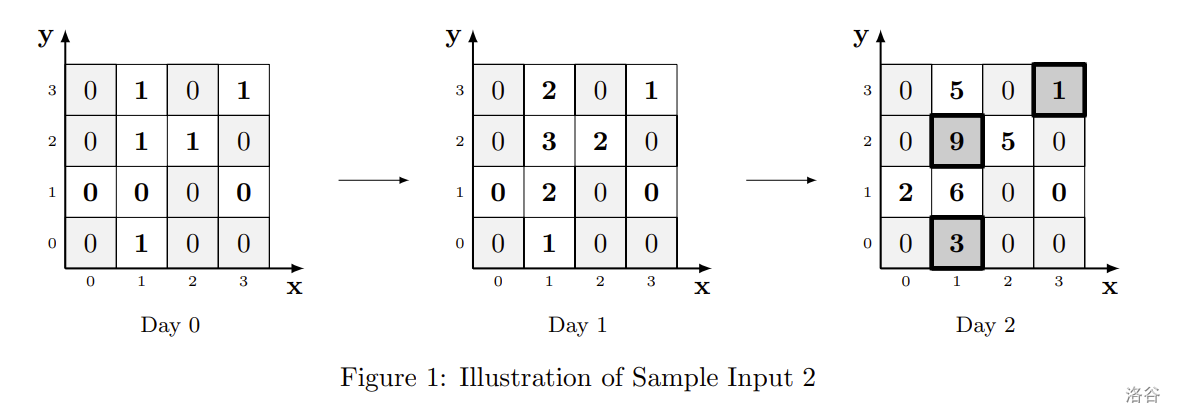
 由 ChatGPT 4.1 翻译