P13660 [CERC 2020] Roof Escape

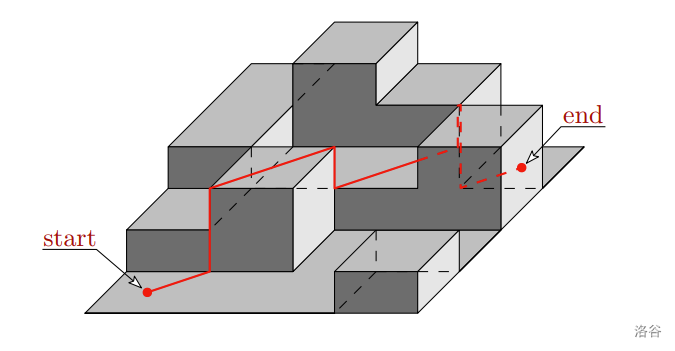
在城市屋顶上逃避警察常常非常棘手，因此匪徒们必须经过适当的训练。为了跟上当前犯罪领域的 AI 趋势，他们正在开发一个通用的计算机化逃跑路模型。 在该模型中，发生逃跑的城市区域被建模为一个由矩形立方体组成的三维网格，这些立方体的底面为正方形，在平坦的地面上形成一个二维网格。每个立方体代表一栋房屋。立方体的顶面称为屋顶。在模型中，相邻街区之间的距离被简化为 $0$。匪徒的逃跑路被建模为一条折线——由一系列水平和垂直的直线段组成，其中一个线段的终点是下一个线段的起点。基本的路径属性如下： - 路径上的每个点都位于至少一个街区的表面上。 - 路径的任何部分都不在任何街区的内部。 - 路径上任意一点的高度大于等于该点所属于的所有街区屋顶的最低高度。 - 路径的起点和终点都在某个街区屋顶的中心。 - 路径所有水平线段长度之和应尽可能小。 可能会出现路径上两个连续线段有公共点的情况。这是因为路径模拟了人在实际物理障碍物上的移动行为。因此，还需满足以下额外的路径规则： - 设 $P$ 为路径上的一个点。如果存在点 $Q$ 恰好在 $P$ 的正上方，且 $Q$ 属于至少两个街区，则点 $Q$ 也在路径上。 需要在模型中精确计算逃跑路的总长度。 

输入的第一行包含六个正整数 $W, H, S_x, S_y, E_x, E_y$（$1 \leq W \cdot H \leq 10^5$，$1 \leq S_x, E_x \leq W$，$1 \leq S_y, E_y \leq H$）。$W$ 和 $H$ 是偶数，表示网格底面的尺寸（单位为米）；$S_x, S_y$ 表示逃跑路起点的坐标，$E_x, E_y$ 表示终点的坐标。 接下来的 $H/2$ 行，每行包含 $W/2$ 个整数，第 $j$ 行的第 $i$ 个整数表示对应街区 $T_{i,j}$ 的高度（单位为米，$0 \leq T_{i,j} \leq 10^3$）。 每个网格街区的底面为 $2 \times 2$ 米的正方形。

输出逃跑路的长度。输出的长度与精确长度的误差必须小于 $10^{-4}$。

样例输入及其解如上图所示。 由 ChatGPT 4.1 翻译