P13666 [GCPC 2023] Adolescent Architecture 2

三年前，你曾帮助小彼得将他的玩具积木堆成一座高塔。从那以后，他扩充了自己的玩具积木收藏，如今拥有以下几种基础形状： - $\texttt{circle}\;a$ —— 半径为 $a$ 的圆形； - $\texttt{square}\;a$ —— 边长为 $a$ 的正方形； - $\texttt{triangle}\;a$ —— 边长为 $a$ 的等边三角形。 其中，$a$ 可以是任意正整数。每个积木的顶部和底部形状相同，因此这些积木分别是长方体、圆柱体和三棱柱。彼得拥有无限数量的每种形状和尺寸的积木。  :::align{center} 图 A.1：游戏进行中。 ::: 彼得和他的朋友 Amy 正在玩一个双人游戏，规则是将积木依次堆叠在一起。 一开始，地板上已经放置了一些积木。 每一回合，当前玩家必须从无限的积木中选择一个，并将其放在现有某一堆的顶部。 在放置之前，积木可以绕其竖直轴旋转。 新积木的轮廓必须严格位于旧积木的轮廓之内，轮廓之间不能接触。 无法进行操作的第一个玩家判负。 给定初始状态，求先手玩家的必胜步数。

输入包括： - 第一行包含一个整数 $n$（$1 \le n \le 1000$），表示初始堆的数量。 - 接下来 $n$ 行，每行包含一个字符串 $s$（$s$ 为 "$\texttt{circle}$"、"$\texttt{square}$" 或 "$\texttt{triangle}$" 之一）和一个整数 $a$（$1 \le a \le 10^9$），描述每一堆顶部的积木。

输出一个整数，表示先手玩家的必胜步数。

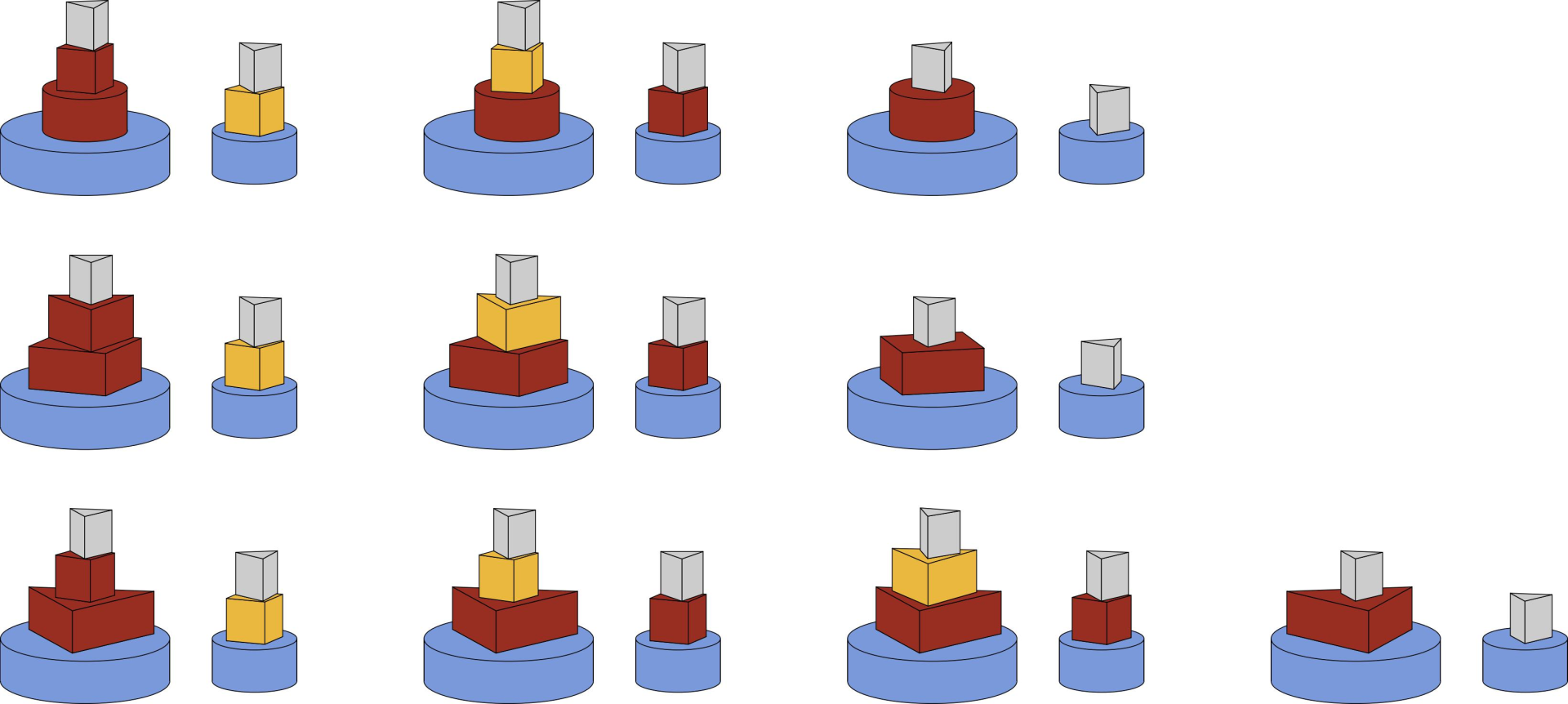
 图 A.2：样例输入 2 的示意图，展示了当彼得先手并采取最优策略时，游戏所有可能的结束状态。蓝色积木为初始状态。彼得需要在 $\texttt{circle\;2}$ 上放置 $\texttt{circle\;1}$、$\texttt{square\;2}$ 或 $\texttt{triangle\;3}$ 中的任意一个，才能获胜。这三种选择分别对应图中的三行。彼得放置的积木用红色表示，Amy 放置的积木用黄色表示。由于最后两个积木总是 $\texttt{triangle\;1}$，因此用灰色表示。例如，如果彼得首先放置 $\texttt{circle\;1}$（如第一行所示），那么彼得可以通过镜像 Amy 的后续操作来获胜。 由 ChatGPT 4.1 翻译