P13677 [GCPC 2023] Loop Invariant

Luna, a historian, was exploring the archives of an old monastery when she stumbled on a mysterious scroll of parchment. On it were only two types of symbols: '$\texttt{(}$' and '$\texttt{)}$'. Soon she noticed that the sequence of symbols satisfies an interesting property: It can be constructed by repeatedly inserting '$\texttt{()}$' at some position into an initially empty sequence. Historians call such sequences *balanced*. Figure L.1 gives an example of a balanced sequence. :::align{center}  Acircular piece of parchment. 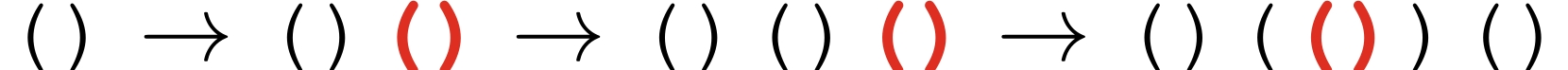:::  :::align{center} Figure L.1: Sample Input 2 derived by successively inserting '$\texttt{()}$' into an initially empty sequence. ::: The chief librarian of the monastery recently told Luna that some of the more elitist monks in the region had a habit of writing on circular pieces of parchment. In their minds, anyone incapable of immediately telling where the text on such a scroll started was also unworthy of knowing its content. Consequently, Luna quickly inspected the edges of her parchment strip. And sure enough, the edges at the left and right end of the parchment strip fit together perfectly, indicating that the parchment once actually was circular. While holding the left and right edges together and looking at the now circular parchment, she wonders whether the balanced sequence starting at the tear is the only such sequence that could have resulted from tearing the parchment apart. After all, it makes little sense trying to decrypt a text when you do not even know where it starts.

The input consists of: - One line with a balanced sequence $s$ ($2\leq |s|\leq 10^6$), the sequence on Luna's strip of parchment.

Output "$\texttt{no}$" if there is no way to obtain a different balanced sequence by cutting the circular sequence, otherwise give any such sequence.