P13732 【MGVOI R1-D】图上的数(graph)
题目描述
你有一张有向图 $G$,这张图中有着无穷多个节点,这些节点的编号为 $1,2,3,...$。
对于任意两个正整数 $i,j$ 而言,当且仅当 $i$ 是 $j$ 的倍数,并且 $i \neq j$ 时,在图 $G$ 中存在一条由 $i$ 号节点指向 $j$ 号节点的边(其长度为 $1$)。
* 下图为 $G$ 中前 $6$ 号节点的状态示例:(点击查看)
::::info[示例]
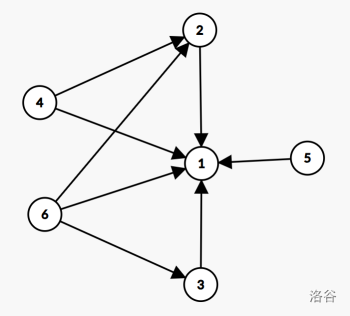
::::
---
对任意的正整数 $x$,给出如下定义:
1. 从 $x$ 号节点到 $1$ 号节点的 **最长路径的长度** 为 $E(x)$;
2. 从 $x$ 号节点到 $1$ 号节点的 **最长路径的条数** 为 $T(x)$;
3. 设在所有满足 $E(y)=E(x)$ 的正整数 $y$ 中,$T(y)$ 的最大值为 $\max \{ T(y) \}$,则定义 $A(x)$ 的值为 $\dfrac{\max \{ T(y) \} }{T(x)}$;
4. 特殊地,规定 $E(1)=0$,$T(1)=A(1)=1$。
可以证明,$A(x)$ 一定是正整数。以下是几个便于你理解上述定义的例子:(点击查看)
::::info[示例]
1. $E(6)=2$,$T(6)=2$,因为从 $6$ 号节点到 $1$ 号节点最多可以经过 $2$ 条边,其对应的 $2$ 条最长路径分别为 $6\rightarrow 3\rightarrow 1$ 和 $6\rightarrow 2\rightarrow 1$。同理可知,$E(4)=2$,$T(4)=1$。
2. $A(6)=1$,因为在所有满足 $E(y)=2$ 的正整数 $y$ 中,可以证明,$T(y)$ 的最大值即为 $2$,与 $T(6)$ 恰好相等。
3. $A(4)=2$,因为在所有满足 $E(y)=2$ 的正整数 $y$ 中,$T(y)$ 的最大值 $2$ 恰好为 $T(4)$ 的 $2$ 倍。
::::
---
给定一个正整数 $N=a^b$,在此基础上,你可以按如下规则构造出一个 $N$ 行 $N$ 列的方格图 $S_N$。
对于正整数 $i,j$($1\le i,j\le N$)而言:
* 当 $N$ 是 $i$ 的倍数,**并且** $i$ 是 $j$ 的倍数时,第 $i$ 行第 $j$ 列的方格上写有数字 $i\times j\times A(j)$;
* 否则,第 $i$ 行第 $j$ 列的方格上写有数字 $1$。
不难验证 $A(1)=A(2)=A(3)=A(6)=1$。以下是方格图 $S_6$ 的示例:(点击查看)
::::info[示例]
|$1$|$1$|$1$|$1$|$1$|$1$|
|:-:|:-:|:-:|:-:|:-:|:-:|
|$2$|$4$|$1$|$1$|$1$|$1$|
|$3$|$1$|$9$|$1$|$1$|$1$|
|$1$|$1$|$1$|$1$|$1$|$1$|
|$1$|$1$|$1$|$1$|$1$|$1$|
|$6$|$12$|$18$|$1$|$1$|$36$|
::::
---
你需要回答以下两个问题:
* 第一问:$A(N)$ 的值是多少?
* 第二问:在方格图 $S_N$ 中,所有方格上数字的总和是多少?
由于答案可能很大,请将所有答案对 $10^9+7$ 取模。
输入格式
**每个测试点包含多组测试数据,各组测试数据之间相互独立。**
第一行包含一个正整数 $T$,表示测试数据的组数。
对于每组测试数据:仅输入一行,包含两个正整数 $a,b$,表示给定的正整数 $N=a^b$。
输出格式
对于每组测试数据:仅需在单独一行输出两个非负整数,用空格隔开,分别表示第一问和第二问的答案(均需对 $10^9+7$ 取模)。
::::warning[注意事项]{open}
即使你不回答其中一问,也需要在对应位置上输出一个小于 $10^9+7$ 的非负整数,以满足输出格式。
本题通过 Special Judge 实现两问分别计分,关于具体的分值分配,请参阅【数据范围】板块。
::::
说明/提示
**【样例 #1】**
::::info[样例 #1 解释]
该样例下,$N=6^1=6$。
在【题目描述】中已经解释过 $A(6)=1$(**即第一问的答案**),并画出了方格图 $S_6$,其中所有方格上数字的总和为 $118$(**即第二问的答案**)。
::::
**【样例 #2】**
::::info[样例 #2 解释(第二组测试数据)]
对于第二组测试数据,$N=2^3=8$。
:::success[第一问的答案说明]
首先可以得到 $E(8)=3$,$T(8)=1$,对应的唯一一条最长路为 $8\rightarrow 4\rightarrow 2\rightarrow 1$。
其次,在所有满足 $E(y)=3$ 的正整数 $y$ 中,有 $\max \{ T(y) \} =6$(详细说明见下),故 $A(8)=\dfrac{6}{T(8)}=6$(**即第一问的答案**)。
当 $y=30$ 时,有 $E(y)=3$,$T(y)=6$,其对应的 $6$ 条最长路分别为:
* $30\rightarrow 15\rightarrow 5\rightarrow 1$;
* $30\rightarrow 15\rightarrow 3\rightarrow 1$;
* $30\rightarrow 10\rightarrow 5\rightarrow 1$;
* $30\rightarrow 10\rightarrow 2\rightarrow 1$;
* $30\rightarrow 6\rightarrow 3\rightarrow 1$;
* $30\rightarrow 6\rightarrow 2\rightarrow 1$。
可以证明,$T(30)=6$ 就是在所有满足 $E(y)=3$ 的正整数 $y$ 中,$T(y)$ 的最大值。
:::
:::success[第二问的答案说明]
列出 $A(x)$ 的值表:
|$x$|$1$|$2$|$4$|$8$|
|:-:|:-:|:-:|:-:|:-:|
|$A(x)$|$1$|$1$|$2$|$6$|
接下来,画出方格图 $S_8$:
|$1$|$1$|$1$|$1$|$1$|$1$|$1$|$1$|
|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|
|$2$|$4$|$1$|$1$|$1$|$1$|$1$|$1$|
|$1$|$1$|$1$|$1$|$1$|$1$|$1$|$1$|
|$4$|$8$|$1$|$32$|$1$|$1$|$1$|$1$|
|$1$|$1$|$1$|$1$|$1$|$1$|$1$|$1$|
|$1$|$1$|$1$|$1$|$1$|$1$|$1$|$1$|
|$1$|$1$|$1$|$1$|$1$|$1$|$1$|$1$|
|$8$|$16$|$1$|$64$|$1$|$1$|$1$|$384$|
所有方格上数字的总和为 $577$(**即第二问的答案**)。
:::
::::
---
::::info[样例 #2 解释(第三组测试数据)]
对于第三组测试数据,$N=6^2=36$。
分析可知 $E(36)=4$,$T(36)=6$。而在所有满足 $E(y)=4$ 的正整数中,取 $y=210$ 即可最大化 $T(y)$,有 $\max \{ T(y) \} =T(210)=24$,据此可得到 $A(36)=\dfrac{T(210)}{T(36)}=4$(**即第一问的答案**)。
由于方格图 $S_{36}$ 的篇幅过大,下面仅画出其最后一行(也就是第 $36$ 行)的状态,并标出列编号:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 |
| :-----------: | :-----------: | :-----------: | :-----------: | :-----------: | :-----------: | :-----------: | :-----------: | :-----------: | :-----------: | :-----------: | :-----------: | :-----------: | :-----------: | :-----------: | :-----------: | :-----------: | :-----------: | :-----------: | :-----------: | :-----------: | :-----------: | :-----------: | :-----------: | :-----------: | :-----------: | :-----------: | :-----------: | :-----------: | :-----------: | :-----------: | :-----------: | :-----------: | :-----------: | :-----------: | :-----------:
| $36$ | $72$ | $108$ | $288$ | $1$ | $216$ | $1$ | $1$ | $648$ | $1$ | $1$ | $864$ | $1$ | $1$ | $1$ | $1$ | $1$ | $1296$ | $1$ | $1$ | $1$ | $1$ | $1$ | $1$ | $1$ | $1$ | $1$ | $1$ | $1$ | $1$ | $1$ | $1$ | $1$ | $1$ | $1$ | $5184$ |
在画出完整的方格图后可以验证,$S_{36}$ 中所有方格上数字的总和为 $12021$(**即第二问的答案**)。
:::warning[温馨提示]
请不要忘记将所有答案对 $10^9+7$ 取模!
:::
::::
**【样例 #3】**
见附件中的 ```graph/graph3.in``` 与 ```graph/graph3.ans```。
这个样例满足测试点 $2 \sim 4$ 的限制。
**【样例 #4】**
见附件中的 ```graph/graph4.in``` 与 ```graph/graph4.ans```。
这个样例满足测试点 $5 \sim 6$ 的限制。
**【样例 #5】**
见附件中的 ```graph/graph5.in``` 与 ```graph/graph5.ans```。
这个样例满足测试点 $7 \sim 10$ 的限制。
---
**【数据范围】**
对于所有测试点,保证 $1\le T\le 100$,$1\le a \le 2\times 10^9$,$1\le b \le 2\times 10^3$。
::cute-table{tuack}
| **测试点编号** | $T \le$ | $a \le$ | $b \le$ | **特殊性质** |
|:-:|:-:|:-:|:-:|:-:|
| $1$ | $2$ | $10$ | $1$ | **AB**
| $2\sim 4$ | $20$ | $2\times 10^3$ | $10$ | ^
| $5\sim 6$ | $100$ | $2\times 10^9$ | $2\times 10^3$ | **C** |
| $7\sim 10$ | ^ | ^ | ^ | 无
特殊性质 **A**:保证 $a^b\le 2\times 10^3$,即 $N\le 2\times 10^3$。
特殊性质 **B**:保证存在正整数 $k$($k\le 5\times 10^5$)满足 $E(k)=E(N)$,$T(k)=A(N)\times T(N)$。
特殊性质 **C**:保证 $a$ 是质数(注意:不保证 $N$ 是质数)。
* 分值分配:每个测试点的分值为 $10$ 分。对于单个测试点,如果你的程序对第一问和第二问均回答正确,则获得满分 $10$ 分;若只回答对了第一问,得 $2$ 分;若只回答对了第二问,得 $8$ 分;若两问均未答对(或输出格式错误),得 $0$ 分。