P13740 [NWERC 2024] Binary Search

You are given an undirected graph with $n$ vertices and $m$ edges. Each vertex $v$ has a number $a_v$ written on it. This number is either $0$ or $1$. A *walk* is a sequence $v_1v_2 \dots v_k$ of vertices in the graph such that any two consecutive vertices are connected by an edge. We call a binary sequence $$s = s_1s_2 \dots s_k$$ *walkable* if there is a walk $v_1v_2 \dots v_k$ in the graph that satisfies $a_{v_1} a_{v_2} \dots a_{v_k} = s$. In other words, a binary sequence is walkable if it is possible to obtain $s$ by walking in the graph and writing down the binary numbers in the order that they are visited. An example is visualized in Figure B.1. 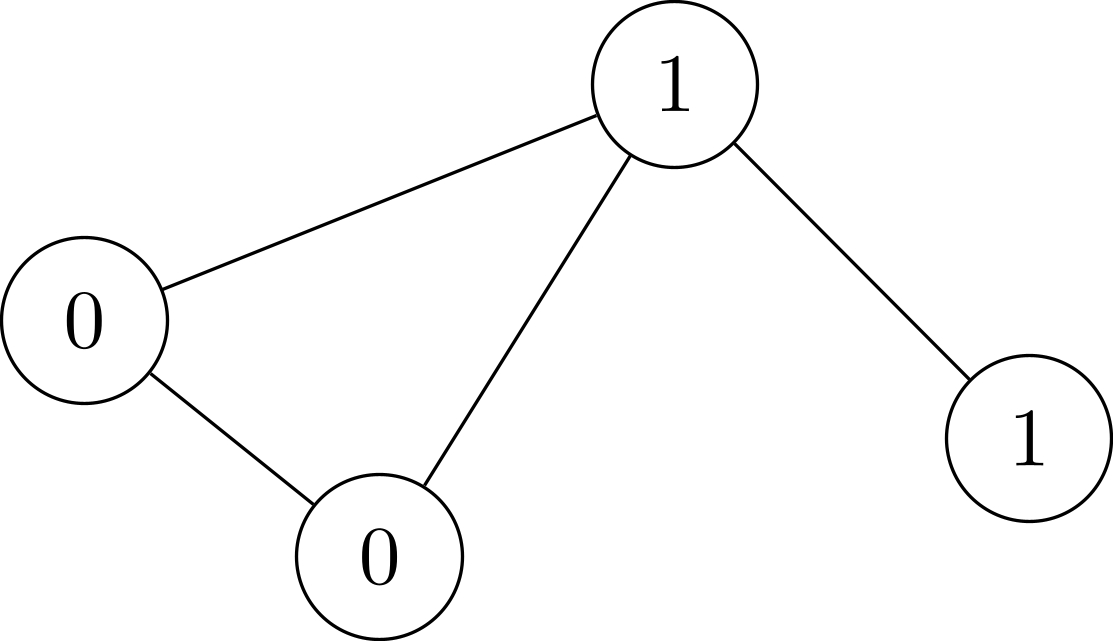:::align{center}  Figure B.1: Illustration of Sample Input 1. Every binary sequence of length at most 3 is walkable. ::: Your task is to find the length of a shortest binary sequence that is not walkable.

The input consists of: - One line with two integers $n$ and $m$ ($1 \leq n \leq 3 \cdot 10^5$, $0 \leq m \leq 3 \cdot 10^5$), the number of vertices and the number of edges. - One line with $n$ integers $a_1,\dots, a_n$ ($a_v \in \{0, 1\}$ for each $v$), where $a_v$ is the number written on vertex $v$. - $m$ lines, each with two integers $u$ and $v$ ($1 \leq u,v \leq n$, $u \neq v$), denoting that the vertices $u$ and $v$ are connected by an edge. It is guaranteed that every pair of vertices is connected by at most one edge.

If every binary sequence is walkable, output "$\texttt{infinity}$". Otherwise, output the length of a shortest binary sequence that is not walkable.