P13745 [NWERC 2024] Glued Grid

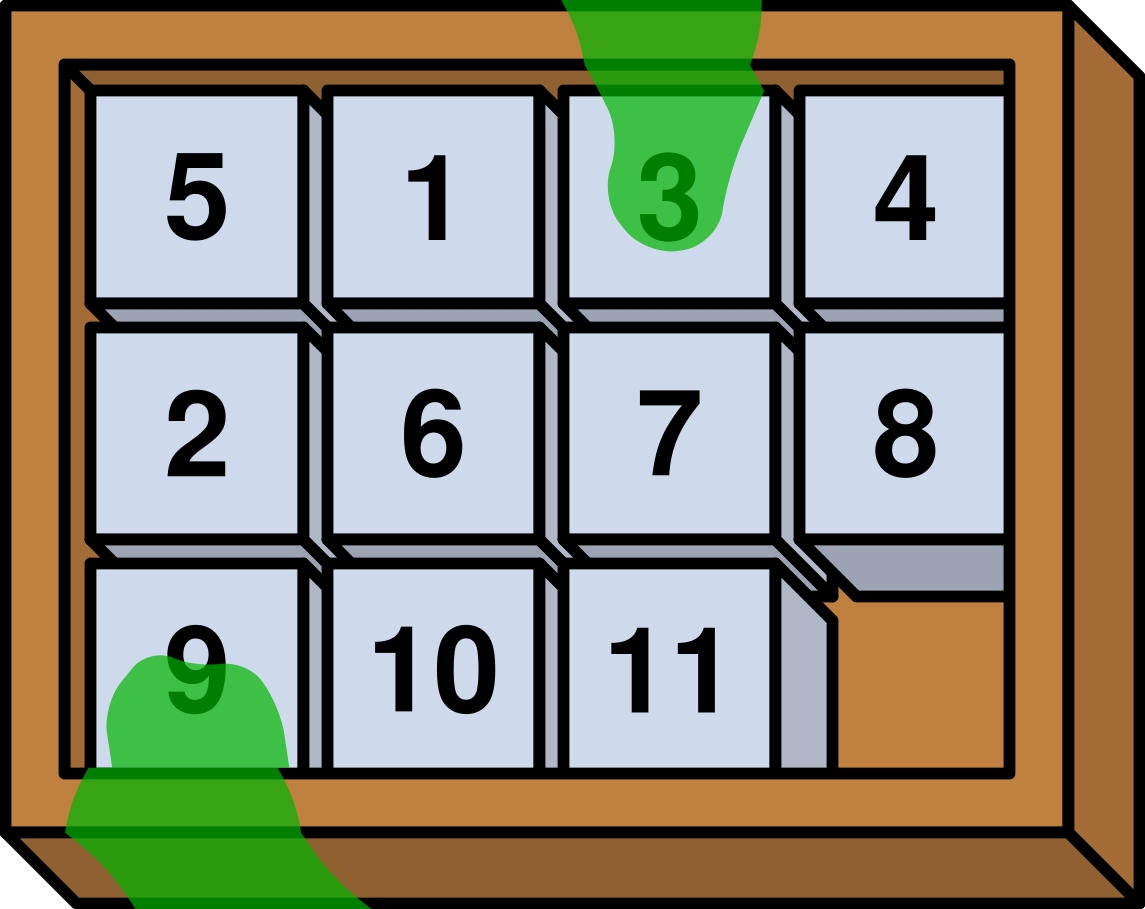
滑块拼图由一个矩形网格上的方形瓷砖组成。网格中恰好有一个位置是空的，你可以将其上方、下方、左侧或右侧的瓷砖移动到空格中，反之亦然。 每个瓷砖上都标有唯一的数字，如图 G.1 所示。要解开滑块拼图，你需要找到一系列移动操作，使得瓷砖编号按从左到右、从上到下的顺序递增排列，并且空格最终位于网格的右下角，如图 G.2 所示。并非所有滑块拼图都存在这样的移动序列。 :::align{center} |  |  |  | |:-:|:-:|:-:| | 图 G.1：一个 $3 \times 4$ 的滑块拼图示例，对应样例输入 1。 | 图 G.2：图 G.1 的滑块拼图被解开后的状态。 | 图 G.3：带有被粘住瓷砖（绿色胶水覆盖）的滑块拼图示例。该示例可被解开，对应样例输入 3。 | ::: 在清理你的车库时，你与车库妖精争夺一个装满好东西的发光盒子。妖精们提出了一个赌注：如果你能解开他们所有的滑块拼图，这个盒子就归你。你决定试一试，却发现妖精们用胶水把一些瓷砖粘在了原地！被粘住的瓷砖无法再移动，如图~\ref{fig:gluedpossible} 所示。 然而，所有滑块拼图都满足以下性质： - 空格位于右下角。 - 每个被粘住的瓷砖都在其正确的位置上。 - 对于每一个可以移动的瓷砖，存在一系列移动操作，使得空格仍然保持在原位。 - 从任意一个被粘住的瓷砖出发，只经过被粘住的瓷砖（每次可向上、下、左、右移动），总能到达滑块拼图的边界。也就是说，没有被粘住的瓷砖被可移动瓷砖完全包围。 请判断给定的滑块拼图是否可以被解开。

输入包括： - 一行包含两个整数 $h$ 和 $w$（$1 \le h,w \le 500$），分别表示滑块拼图的高度和宽度。 - 接下来 $h$ 行，每行包含 $w$ 个字符，每个字符为 '$.$' 或 '$\#$'。右下角的位置（空格）为 '$.$'。其余位置，'$.$' 表示可移动的瓷砖，'$#$' 表示被粘住的瓷砖。 - 接下来 $h$ 行，每行包含 $w$ 个整数 $a_{i,j}$（$1 \le i \le h$, $1 \le j \le w$, $0 \le a_{i,j} \le h \cdot w - 1$）。右下角的整数为 $a_{h,w} = 0$，表示空格。其余 $a_{i,j}$ 表示位置 $(i,j)$ 上瓷砖的编号。 所有 $a_{i,j}$（$1 \le i \le h, 1 \le j \le w$）的集合恰好包含 $0, 1, \dots, h \cdot w - 1$ 各一次。

如果滑块拼图可以被解开，输出 "possible"；否则输出 "impossible"。

由 ChatGPT 4.1 翻译