P13747 [NWERC 2024] It's a Kind of Magic

众所周知，一个 $3\times3$ 的幻方必须满足两个条件： 1. 九个数字都必须是正整数且互不相同。 2. 每一行、每一列以及两条对角线上的数字之和都相等。 除了 Matt Parker$^1$ 之外，大家都知道这些。 他想要创造一个“平方幻方”，也就是在幻方的基础上再加上第三个条件： 3. 每个数字都是某个正整数的平方。 他的“成果”可以在右上角的图片中看到。 你可能已经注意到，他的幻方并不那么“神奇”……不仅大多数数值出现了两次，而且还有一条对角线的和不正确。 说实话，除了包含了非平方数之外，这个幻方几乎没有什么可以更糟糕的地方了。 不过，至少他尝试过了！ :::align{center}  Parker Square。© [Brady Haran](https://www.bradyharanblog.com/the-parker-square)，已获授权使用 ::: 但那都是过去的事了。 在发现了 *Parker Square* 之后，他决定从此完全无视条件 $3$，而是对条件 $2$ 进行了新的改编。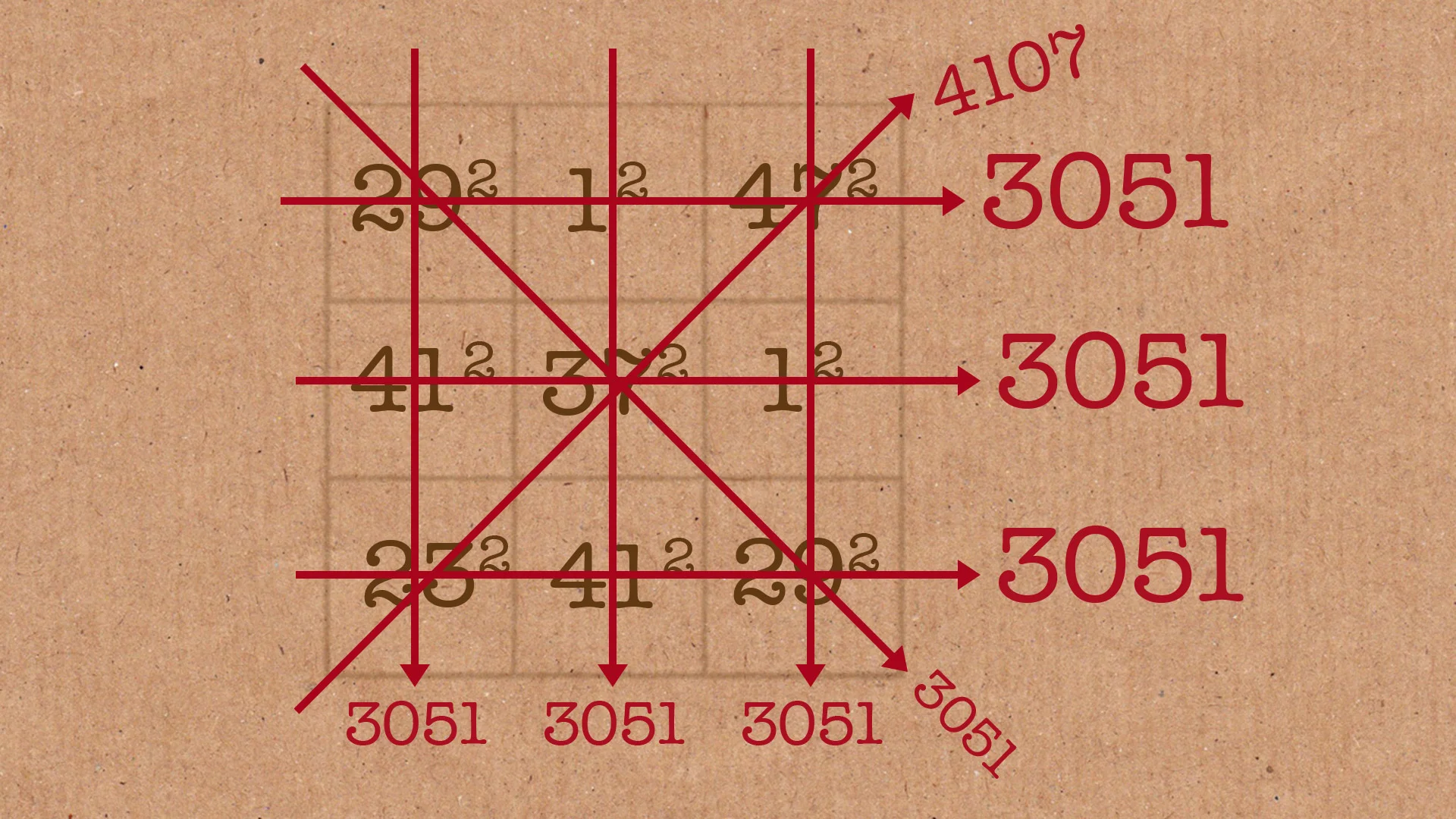 他现在考虑“乘法幻方”，也就是与普通幻方类似，但要求每一行、每一列以及两条对角线上的数字之*积*都相等，而不是和相等。 谁知道呢，也许 Matt 以后真的能找到一个合格的乘法幻方！ 有了这个定义，Matt 写了一段糟糕的 Python 代码——这是他自己的评价——用来统计所有单行、单列或对角线上的数字之积不超过 $n$ 的 $3\times3$ 乘法幻方的数量。 你大概已经猜到了，他的代码太慢了。 因此，我们的任务就是高效地完成同样的事情。 给定一个整数 $n$，请你计算所有乘法幻方的数量，要求每一行、每一列或对角线上的数字之积都不超过 $n$。 --- $^1$娱乐数学家、作家、喜剧演员、YouTube 红人及科学传播者。

输入包含： - 一行一个整数 $t$（$1 \leq t \leq 10^5$），表示测试用例数量。 - 接下来 $t$ 行，每行一个整数 $n$（$1 \leq n \leq 10^{18}$），表示单行、单列或对角线上的最大积。

对于每个测试用例，输出一个整数，表示所有乘法幻方的数量，要求每一行、每一列或对角线上的数字之积都不超过 $n$。

由 ChatGPT 4.1 翻译