P13751 [NWERC 2024] Mouse Trap

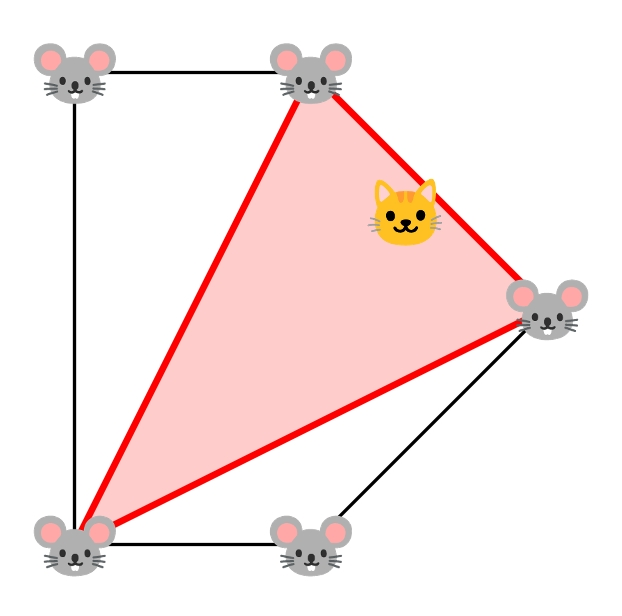
猫咪 Medea 是个名副其实的捣蛋鬼。 虽然她对人类很温柔体贴，但有时候她会为了好玩，未经邀请地闯入她家附近田野里的老鼠聚会！ :::align{center}  Medea 和一只老鼠。 ::: 老鼠聚会是指一群老鼠站在二维平面上一个凸多边形的顶点上。 当 Medea 闯入老鼠聚会时，她会突然跳到多边形内部的某个点上。 所有老鼠和 Medea 都可以视为二维平面上的点，也就是说它们没有形状和尺寸。 不过 Medea 还是很谨慎的。 她会考虑老鼠们是否会把她包围起来，因此她会在老鼠有机会包围她之前逃跑。 Medea 将“包围”定义为：存在恰好三只老鼠，使得以这三只老鼠为顶点构成的三角形将她严格包含在内部。 如图 M.1 所示。 :::align{center}  图 M.1：样例输入 2 的示意图，展示了当 Medea 跳到 $(1.4,1.4)$ 时的三种包围情况之一。 ::: 有一天，Medea 决定去捣乱老鼠们的聚会。 她跳得并不精确，因此她并不知道自己会落在多边形内部的哪个点——她只知道自己会以均匀概率跳到多边形内部的某个实数坐标点。 Medea 想知道，当她落在多边形内部后，期望会有多少种不同的包围情况。 这个问题对 Medea 来说太难了，即使她有 200 的智商也算不出来，于是她向你求助！

输入包括： - 一行一个整数 $n$（$3 \leq n \leq 2\cdot 10^5$），表示老鼠的数量。 - 接下来 $n$ 行，每行两个整数 $x$ 和 $y$（$|x|, |y| \leq 10^7$），表示一只老鼠的坐标。 老鼠的坐标按逆时针顺序给出，并且构成一个严格凸多边形且面积非零。严格凸多边形指的是没有任意三个连续顶点共线的凸多边形。

输出 Medea 落在多边形内部后，期望出现的不同包围情况的数量。 你的答案的绝对误差或相对误差不超过 $10^{-4}$。

由 ChatGPT 4.1 翻译