P13764 [CERC 2021] Building on the Moon

ICPC 教练们从未真正退休。当他们宣布“退休”时，实际上是开始为一个秘密机构工作（我们不能透露更多细节），该机构正在月球背面建造宏伟的建筑。目前有一个这样的项目正在进行中。 为了建造这座宏伟的建筑，他们可以使用两种不同类型的六边形建筑模块： - 一个“房间”有三个开口，分别位于它的三条互不相邻的边上。 - 一个“连接件”有两个开口，分别位于两条相对的边上。 两个连接件（或一个连接件和一个房间）可以沿着有开口的边连接在一起；然后这些结构会被焊接，使其密封。 计划是在月球表面建造一个包含 $N$ 个房间的建筑。每个房间都通过通道与恰好三个其他房间相连。每条通道由 $L$ 个连接件首尾相连组成。每条通道的两端（即开口所在的位置）都连接在一个房间上。例如，假设有 $N=4$ 个房间，编号为 1 到 4，且 $L=3$。一种可能的结构如下图所示（房间用灰色阴影表示）： :::align{center}  ::: 保证任意一对房间之间至多有一条通道相连，且没有通道连接同一个房间。同时，建筑内部任意两房间之间都可以通过通道互达。此外，方案由前 CERC 教练设计，保证通道之间不会相交（记住结构是在月球表面建造的）。这样的方案可以用一系列三元组描述： $$\left(c_{1}^{(1)}, c_{2}^{(1)}, c_{3}^{(1)}\right),\left(c_{1}^{(2)}, c_{2}^{(2)}, c_{3}^{(2)}\right), \ldots,\left(c_{1}^{(n)}, c_{2}^{(n)}, c_{3}^{(n)}\right)$$ 这表示第 $i$ 个房间分别与 $c_{1}^{(i)}$、$c_{2}^{(i)}$ 和 $c_{3}^{(i)}$ 号房间通过通道相连。如果一个人站在编号为 $i$ 的房间内，顺时针旋转一圈，他会依次看到通往 $c_{1}^{(i)}$、$c_{2}^{(i)}$ 和 $c_{3}^{(i)}$ 的通道。上述方案可以描述为如下序列： $$ (2,3,4),(1,4,3),(1,2,4),(1,3,2) $$ 由于月球背面很黑暗（正如其名字所暗示），每个建筑模块（无论是房间还是连接件）的每一条边上都要安装一根霓虹灯管。当然，两个模块焊接在一起的边上只安装一根霓虹灯管。由于结构建在月球上，我们不能浪费太多能源，因此不能同时点亮任何两根相邻的霓虹灯管。教练们决定，为了提供足够的照明，他们将点亮在节能约束下最多数量的霓虹灯管。这样的点亮方式称为“有效点亮”，而且可能有多种方案。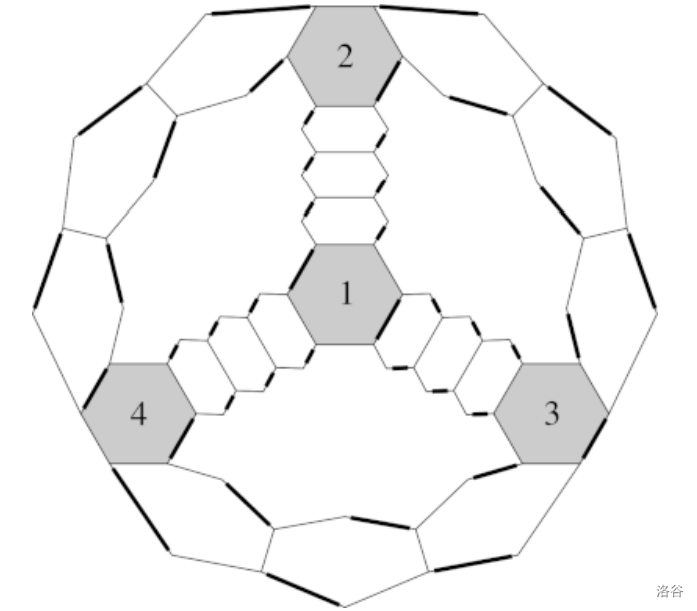下图展示了一种可能的方案： :::align{center}  ::: 教练们认为还有许多其他方式可以实现这一点。他们现在想知道，有多少种不同的有效点亮方式。由于答案可能非常大，请输出答案对 $10^6+3$ 取模的结果。

第一行包含两个用空格分隔的整数 $N$ 和 $L$，分别表示房间的数量和每条通道中连接件的数量。接下来 $N$ 行，每行包含三个用空格分隔的整数 $c_{1}^{(i)}, c_{2}^{(i)}, c_{3}^{(i)}$。

输出一个整数，表示有效点亮方式的总数，对 $10^6+3$ 取模。

### 输入范围 - $4 \leq N \leq 16$ - $1 \leq L \leq 100$ - $1 \leq c_{j}^{(i)} \leq N$，其中 $j=1,2,3$，$i=1,2,\ldots,N$。 由 ChatGPT 4.1 翻译