P13769 [CERC 2021] Lines in a grid

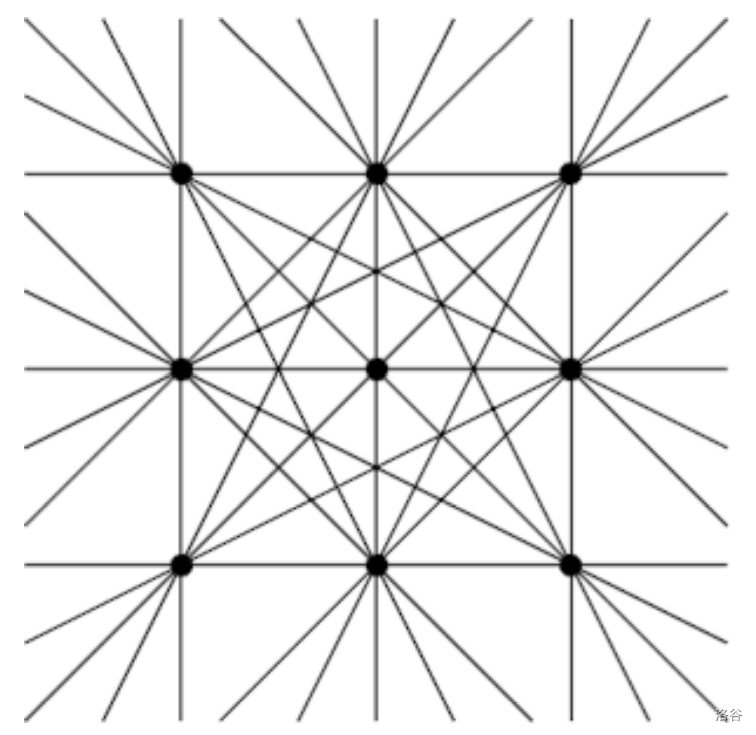
Suppose that we are given a $n \times n$ integer grid, e.g. $\{(i, j)\}_{i=0, j=0}^{n-1, n-1}$. Let $l_n$ be the number of different lines that intersect with at least two points on the grid. For $n = 3$, there are exactly 20 such lines, as drawn on the image below. :::align{center}  ::: Compute $l_n$ for all given $n$.

First line contains an integer $Q$ – the number of queries. The second line contains $Q$ space-separated integers $n_1, \ldots, n_Q$.

Print $Q$ numbers $l_{n_1}, \ldots, l_{n_Q}$, each in its own line. Since $l_k$ can be large, print them modulo $10^6 + 3$.

### Input limits * $1 \leq Q \leq 1000$ * $1 \leq n_i \leq 10^7$