P13782 [eJOI 2022] Where Is the Root?

This is an interactive problem

You are given a tree of $n$ vertices. The tree is a graph such that there is exactly one simple path between every pair of vertices. **It's also guaranteed that at least one vertex is directly connected by an edge to at least 3 vertices.** One of the vertices is the root, and your task is to find it. In order to do this, you are allowed to ask queries of the following form: - For a given set $a_1, a_2, \ldots, a_m$ of vertices, check if their lowest common ancestor is in this set. A vertex $v$ is a common ancestor of a set $S$ of vertices if the paths from all vertices in $S$ to the root pass through $v$. The lowest common ancestor (LCA) of a set $S$ of vertices is the common ancestor of $S$ which is farthest from the root. ### Interaction Start the interaction by reading a single integer $n$ ($4 \leq n \leq 500$) - the number of vertices. Then read next $n - 1$ lines. The $i$-th line will contain two integers $a_i, b_i$ ($1 \leq a_i, b_i \leq n$), indicating that there is an edge between vertices $a_i, b_i$ in the tree. It's guaranteed that these $n - 1$ edges form a tree and at least one vertex is directly connected by an edge to at least 3 vertices. To ask a query, firstly output "?", then the integer $m$, and then $m$ distinct integers $a_1, a_2, \ldots, a_m$ ($1 \leq m \leq n, 1 \leq a_i \leq n$, all $a_i$ are distinct) - vertices, for which you want to check if their LCA is among them. As a response, the interactor will output "YES" if their LCA is one of $a_1, a_2, \ldots, a_m$, and "NO" otherwise. You can ask at most 1000 queries, but you'll get a different number of points depending on how many queries you ask. Outputting the answer does not count as a query. Please, look at the scoring section for the details. When you have identified the root, output the symbol "!" and then one integer $v$ ($1 \leq v \leq n$) - the root. Then terminate your program. After printing a query do not forget to output end of line and flush the output. To do this, use: - `fflush(stdout)` or `cout.flush()` in C++; - `stdout.flush()` in Python; It is guaranteed that for each test case, the tree and its root are fixed before the start of the interaction. In other words, the interactor is not adaptive.

N/A

N/A

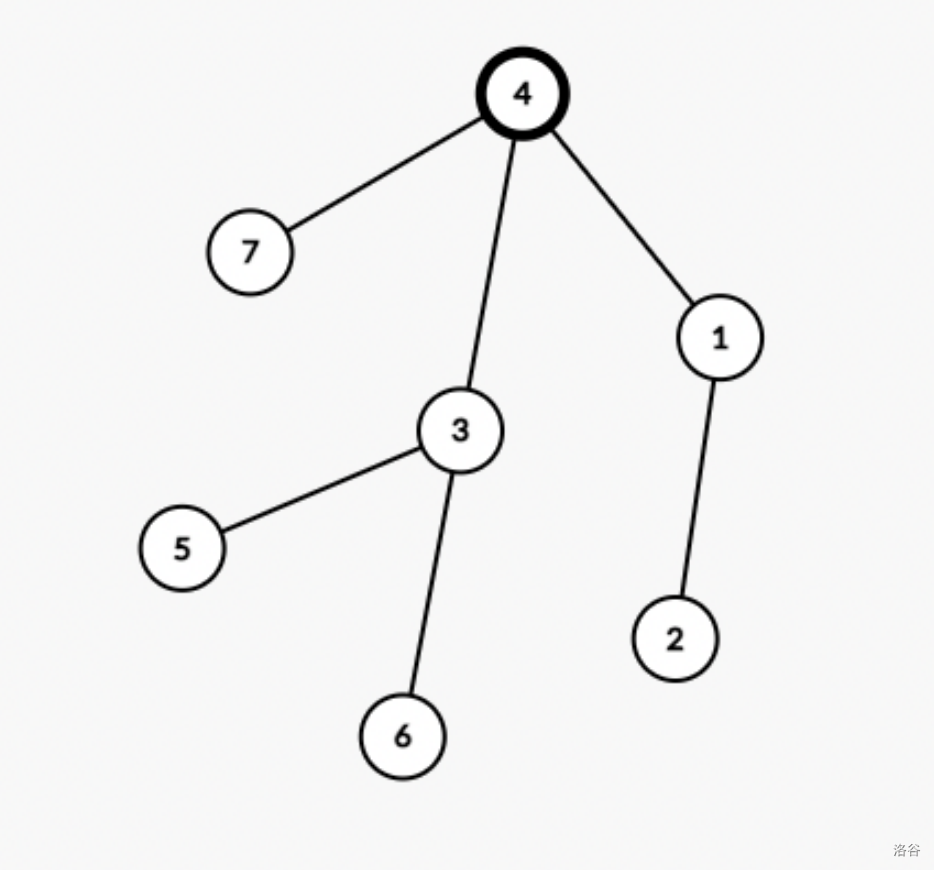
### Note  In the first query, the LCA of vertices 5 and 6 is vertex 3 which is not among vertices 5 and 6 so the answer is "NO". In the second query, the LCA of vertices 3, 5, and 6 is vertex 3 so the answer is "YES". In the third query, the LCA of vertices 1 and 7 is vertex 4 so the answer is "NO". In the fourth query, the LCA of vertices 4 and 6 is vertex 4 so the answer is "YES". After that, we can guess that root is vertex 4 which is the correct answer. ### Scoring 1. (7 points): $n \leq 9$ 2. (10 points): $n \leq 30$ 3. (up to 83 points): $n \leq 500$ In the first and second subtasks you can ask at most 1000 queries. In the third subtask, let $k$ be the maximum number of queries you asked in any test. If $k \leq 9$, you will get 83 points. Otherwise, you will get $\left\lfloor \max \left(10, 83 \cdot \left(1 - \frac{\ln(k-6)}{7}\right)\right) \right\rfloor$ points. C++ code that computes the number of points for the third subtask: ```cpp ((k