P13817 「LDOI R3」球球碰撞

我以爲走下去是一種默契。 你卻說你需要離開，需要一些空間呼吸。

一条一维的无限长轨道上，给定 $n$ 颗弹珠，第 $i$ 颗弹珠有一个**初速度** $v_{i}$。 你需要设置每一颗弹珠的**位置**和**初始方向**，使得： - 初始时任意两颗弹珠不在同一位置。 - **启动装置**后，**不允许**某一时刻，存在 $x(x\ge3)$ 颗弹珠同时在同一位置碰撞。 你需要最大化启动装置后发生的碰撞总数，你只需要求出该值即可，不需要给出具体每个弹珠的位置和初始方向。 **启动装置**后，若任意两颗弹珠运动到同一位置，即称发生了一次无能量损失的碰撞，这两个弹珠会**交换运动方向和速度**。 例如，速度为每秒 $2$ 米的弹珠 A 和每秒 $3$ 米的弹珠 B **迎面相撞**，那么这两个弹珠相互弹开改变方向，并且弹珠 A 速度变为每秒 $3$ 米，弹珠 B 速度变为每秒 $2$ 米。

**本题有多组测试数据。** 第一行，一行一个整数 $T$ 代表数据组数。 接下来包含 $T$ 组数据，每组数据的格式如下： 第一行包含一个正整数 $n$，表示弹珠数量。 第二行包含 $n$ 个正整数 $v_1, v_2, \dots, v_n$，表示每一颗弹珠的速度。

对于每组数据：输出一行包含一个非负整数，表示最大的碰撞数。

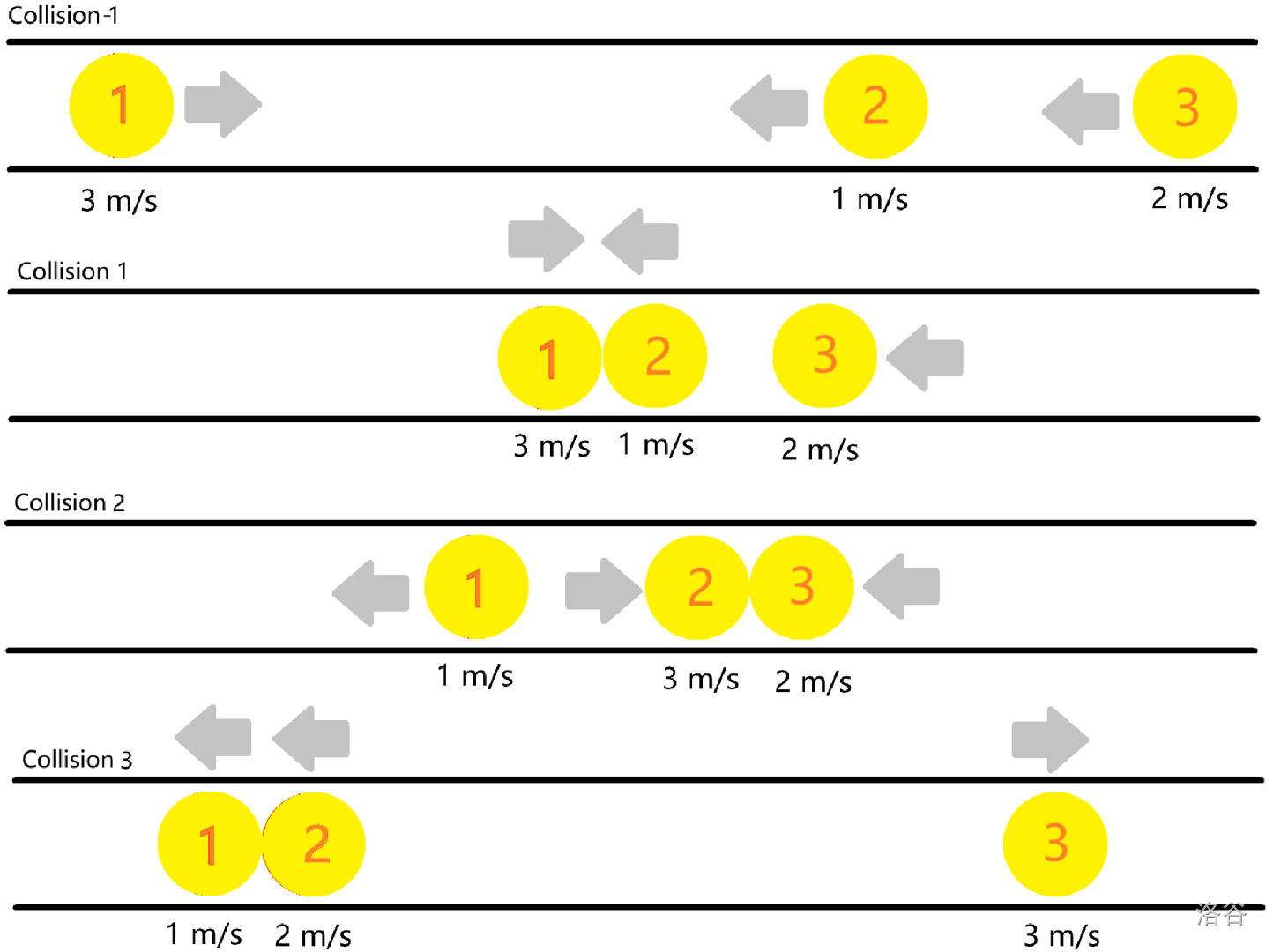
#### 【样例解释】 对于第一组数据，两颗弹珠迎面相撞后相离，不会进行第二次碰撞。碰撞数为 $1$。 对于第二组数据，如下图设置，碰撞数最大为 $3$。可以证明不存在更大的碰撞数。  #### 【数据范围和约定】 **本题使用了子任务依赖。** 对于所有测试数据，保证： - $1\leq T\leq 5$， - $2\leq n\leq 10^5$， - $1\leq v_i\leq 10^9$。 ::cute-table{tuack} | $\text{Subtask}$ | $n$ | $v_i$ | 特殊性质 | 分值 | 子任务依赖 | | :-: | :-: | :-: | :-: | :-: | :-: | | $0$ | $\leq 5$ | $\leq 10$ | 样例 | $0$ | $/$ | | $1$ | $\leq 20$ | $\leq 10^9$ | 无 | $10$ | $0$ | | $2$ | $\leq 2000$ | $\leq 10^9$ | 有 | $10$ | $0$ | | $3$ | $\leq 2000$ | $\leq 10^9$ | 无 | $15$ | $0,1$ | | $4$ | $\leq 10^5$ | $\leq 10^9$ | 有 | $15$ | $0,2$ | | $5$ | $\leq 10^5$ | $\leq 10$ | 无 | $20$ | $0$ | | $6$ | $\leq 10^5$ | $\leq 10^9$ | 无 | $30$ | $0\sim 5$ | 特殊性质：所有的 $v_{i}$ 互不相同。