P13821 「Diligent-OI R2 A」Green, Green the Reed

On a sufficiently large grid, there are $n$ rows of open spaces, where columns $1$ to $a_i$ of row $i$ are all open spaces. Except for the given open space, all other locations are obstacles. You will start from the leftmost cell of the first row $(1,1)$, and reach the rightmost cell of the last row $(n,a_n)$. Movement is restricted to up, down, or right directions within the grid. Cells may be revisited, but each cell is counted only once. Determine the maximum number of distinct cells visited during such a path.

The first line contains an integer $n$. The second line contains $n$ integers $a_1,a_2,\dots,a_n$.

A single integer representing the maximum distinct cells visited.

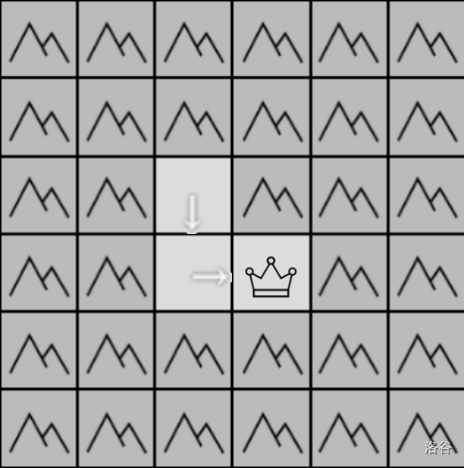
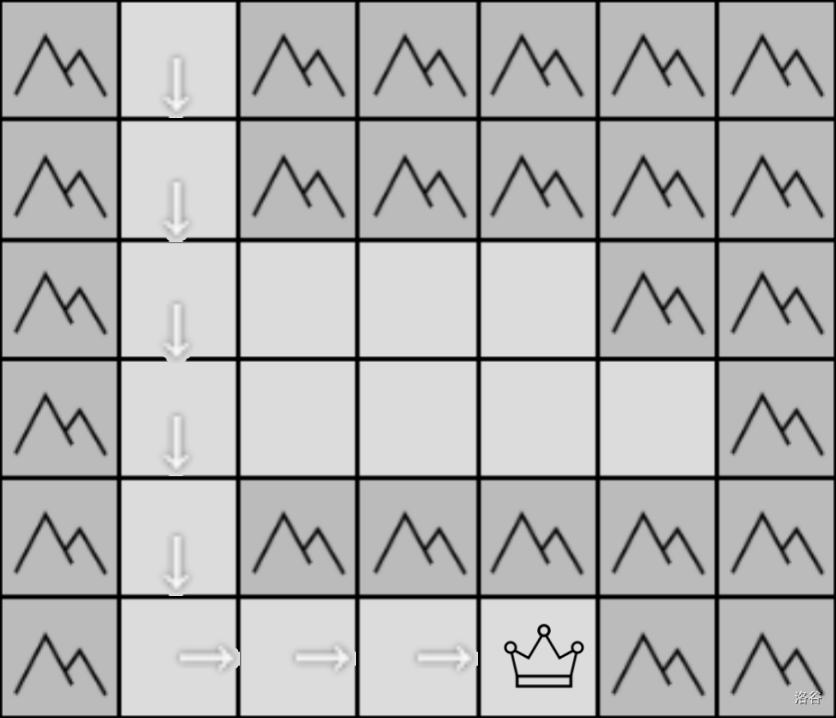
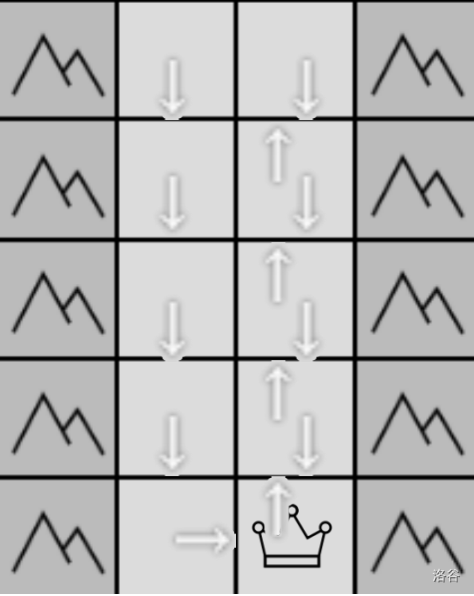
#### Sample #1 Explanation:  Path: $(1,1)\to(2,1)\to(2,2)$. #### Sample #2 Explanation:  Path: $(1,1)\to(2,1)\to(3,1)\to(4,1)\to(5,1)\to(6,1)\to(6,2)\to(6,3)\to(6,4)$. #### Sample #3 Explanation:  Path: $(1,1)\to(2,1)\to(3,1)\to(4,1)\to(5,1)\to(4,1)\to(3,1)\to(2,1)\to(1,1)\to(1,2)\to(2,2)\to(3,2)\to(4,2)\to(5,2)$. (Note: Revisited cells are counted once) #### Data Range All data guarantees: $1\le n\le100,1\le a_i\le100$. - Subtask 1 (20pts): $n=2$. - Subtask 2 (20pts): $a_i\le a_{i+1}$ for all $1\le i