P13824 「Diligent-OI R2 D」Beyond the Stream

Every time Ns6 attends Dong Gong Ling's course, he brings a pile of snacks, which has long been coveted by Klg and acmp. Therefore, Klg and acmp have devised a secret plan to raid the snacks. The computer lab is fraught with danger. Will Ns6 be able to escape this ordeal?

The computer lab is enormous and intricately structured. It contains $n$ junction points, each described by two parameters $x_i,y_i$. The podium is also considered a junction point, numbered $1$. The "NC2 distance" from the $i$-th junction point to the $j$-th junction point is $(x_i-x_j)^2+(y_i-y_j)^2$. There are $n-1$ bi-directional passages connecting all junction points, forming a tree with the podium as the root. **The length of each passage is the "NC2 distance" between the connected junction points.** People can only walk along passages and cannot divert into another passage midway. However, snacks can be thrown and passed between two points with an "NC2 distance" of no more than $d$. Klg and acmp's raiding plan is as follows: - They select two junction points $p,q$ (with $p\le q$). Klg starts at $p$ and acmp starts at $q$. The shortest **path formed by passages** connecting $p$ and $q$ is the "activity path". - Each time, they pass snacks between them, requiring the "NC2 distance" between their current junction points to not exceed $d$. Note that they must also pass snacks when they are initially at $p$ and $q$. - After each snack pass, **at least one of them must move exactly one passage toward the podium** before the next snack pass. However, **both must remain on the "activity path" throughout**. - The raid stops and is considered successful when they are at the same junction point during a snack pass. Klg and acmp have planned $t$ raids, with $d$ potentially changing each time. Ns6 needs to know, for each plan, if it can succeed, what is the maximum possible length of the "activity path" (i.e., the sum of the lengths of each passage on the "activity path")? Please output $p,q$ under this condition. If there are multiple solutions, output the one with the smallest $p$, and if still multiple, the one with the smallest $q$. **Note that the distance between two points in this problem is "NC2 distance", not Euclidean distance.**

The first line contains two integers $n,t$. The next $n$ lines each contain two integers $(x_i,y_i)$. The next $n-1$ lines each contain two integers $u,v$ representing a passage connecting junction points $u$ and $v$. The next $t$ lines each contain one integer representing $d$ for that query.

Output $t$ lines, each containing two integers representing the satisfying $p,q$.

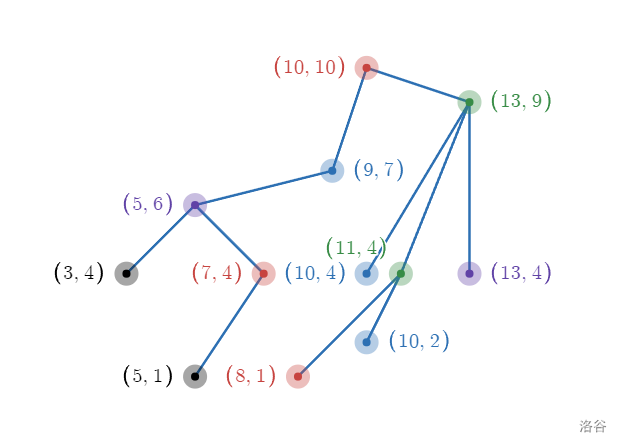
#### Sample #1 Explanation: The structure of the computer lab in the sample is as follows:  Taking the first raid as an example: The $x,y$ of points $7$ and $12$ are $(10,4)$ and $(10,2)$, respectively. The length of the active path between $7$ and $12$ is $34+29+5=68$. Initially, the two are at $7$ and $12$, with an "NC2 distance" of $4$. In the second step, they are at $7$ and $8$, with an "NC2 distance" of $1$. In the third step, they are both at $3$, and the raid ends. It can be proven that there is no better solution. #### Data Range All data guarantees: $3\le n\le 1000,1\le t\le 10^5,0\le x_i,y_i\le 10^6,0\le d\le2\times10^{12}$. - Subtask 1 (20pts): $n\le10,t\le5$. - Subtask 2 (15pts): $n\le100,t\le5$. - Subtask 3 (25pts): $t\le5$. - Subtask 4 (10pts): Each junction point is connected to at most two passages. - Subtask 5 (30pts): No special properties.