P13899 [CSPro 28] JPEG 解码
题目背景
洛谷的测试数据仅供民间交流使用,非官方测试数据。官方评测链接:。
四年一度的世界杯即将画上尾声。在本次的世界杯比赛中,视频助理裁判(Video Assistant Referee, VAR)的应用可谓是大放异彩。VAR 使用视频回放技术帮助主裁判作出正确判罚决定。西西艾弗岛足球联赛的赛场上也引入了一套 VAR 设备。作为技术供应商的技术主管小 C,需要存储和编码 VAR 产生的图像数据。小 C 分析比较发现,JPEG 编码算法可以达到较好的压缩效果,并且质量损失是可以接受的。因此,小 C 决定使用 JPEG 编码算法来存储和传输图像数据。JPEG 是一种常用的图片有损压缩算法,它的压缩率高,但是压缩后的图片质量下降较多。JPEG 图片的压缩率一般在 $10:1$ 到 $20:1$ 之间,一般用于存储照片等图片质量要求不高的场景。
为了简化问题,我们以灰度图片为例,介绍 JPEG 编码算法的过程。一张灰度图片,可以被视为由多个像素点组成。每个像素点对应一个 0 到 255 之间的数值,用于表示像素点的亮度。JPEG 编码算法将图片分割为 $8 \times 8$ 的小块,每个小块被称作一个最小编码单元。对每个小块进行如下的计算:
1. 将每个像素点的数值减去 128,使得每个像素点的数值都在 -128 到 127 之间。
2. 将每个小块的像素点排成一个 $8 \times 8$ 的矩阵,并对矩阵进行离散余弦变换(DCT)。进行离散余弦变换后,仍然得到一个 $8 \times 8$ 的矩阵,矩阵中的每个元素都是实数,并且所得矩阵的左上方的数字的绝对值较大,右下方的数字的绝对值较小,甚至接近 0。
3. 对矩阵进行量化操作。量化操作是指将矩阵中的每个元素都除以一个数字,并取整数。量化操作的目的是为了减少矩阵中的数据,从而减少编码后的文件大小。量化操作的数字越大,矩阵中的数据就越少,但是压缩后的图片质量也会越差。
4. 对矩阵进行 Z 字形扫描。Z 字形扫描是指从左上角开始,沿着 Z 字形的路径扫描矩阵中的元素,将扫描到的元素依次排成一个数组,由于 Z 字形扫描的路径是从左上角到右下角,数组结尾处可能存在着连续的 0,为了节省空间,可以不存储这些连续的 0。得到的数据被称为扫描数据。
最后,将得到的各个小块的扫描数据采用哈夫曼编码进行压缩,并置于必要的数据结构中,就能得到一张 JPEG 图片了。
题目描述
在本题中,你需要实现一个能够解码 JPEG 图片的一个最小编码单元的程序。解码的步骤与上述编码的步骤相反,具体的步骤是:
1. 读入量化矩阵 $Q_{i,j}$,其中 $i, j$ 的取值范围为 $0 \sim 7$。
2. 初始化一个 $8 \times 8$ 的矩阵 $M$,令 $M_{i,j} = 0$。
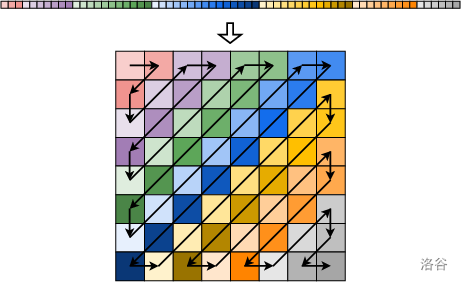
3. 读入扫描数据,将扫描数据按照这样的顺序写入矩阵 $M$:从左上角 $M_{0,0}$ 开始,接下来填充它的右侧相邻的元素 $M_{0,1}$,然后依次向左下方填充直至 $M_{1,0}$,接下来从它下侧相邻的元素 $M_{2,0}$ 开始,依次向右上方填充直至 $M_{0,2}$,依次类推,循环往复,直至填充满整个矩阵或用尽所有扫描数据,如图所示。
:::align{center}
:::
4. 将矩阵 $M$ 中的每个元素都乘以量化矩阵 $Q$ 中的对应元素。
5. 对矩阵 $M$ 进行离散余弦逆变换,得到一个 $8 \times 8$ 的矩阵 $M'$. 其中,逆变换的公式如下:
$$
M'_{i,j} = \frac{1}{4} \sum_{u=0}^{7} \sum_{v=0}^{7} \alpha(u) \alpha(v) M_{u,v} \cos\left(\frac{\pi}{8}(i + \frac{1}{2})u\right) \cos\left(\frac{\pi}{8}(j + \frac{1}{2})v\right)
$$
其中 $\alpha(u) = \begin{cases} \sqrt{\frac{1}{2}} & u = 0 \\ 1 & u \neq 0 \end{cases}$
6. 将矩阵 $M'$ 中的每个元素都加上 128,并取最接近的整数(四舍五入)。如果得到的整数大于 255,则取 255;如果得到的整数小于 0,则取 0。得到的矩阵即为解码后的图片。
例如,假设给定的量化矩阵是:
$$\begin{bmatrix} 16 & 11 & 10 & 16 & 24 & 40 & 51 & 61 \\ 12 & 12 & 14 & 19 & 26 & 58 & 60 & 55 \\ 14 & 13 & 16 & 24 & 40 & 57 & 69 & 56 \\ 14 & 17 & 22 & 29 & 51 & 87 & 80 & 62 \\ 18 & 22 & 37 & 56 & 68 & 109 & 103 & 77 \\ 24 & 35 & 55 & 64 & 81 & 104 & 113 & 92 \\ 49 & 64 & 78 & 87 & 103 & 121 & 120 & 101 \\ 72 & 92 & 95 & 98 & 112 & 100 & 103 & 99 \end{bmatrix}$$
给出的扫描数据是:$-26, -3, 0, -3, -2, -6, 2, -4, 1, -3, 1, 1, 5, 1, 2, -1, 1, -1, 2, 0, 0, 0, 0, 0, -1 -1$,那么填充后的矩阵 $M$ 是:
$$\begin{bmatrix}
-26 & -3 & -6 & 2 & 2 & -1 & 0 & 0 \\
0 & -2 & -4 & 1 & 1 & 0 & 0 & 0 \\
-3 & 1 & 5 & -1 & -1 & 0 & 0 & 0 \\
-3 & 1 & 2 & -1 & 0 & 0 & 0 & 0 \\
1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0
\end{bmatrix}$$
与量化矩阵逐项相乘后的矩阵是:
$$\begin{bmatrix}
-416 & -33 & -60 & 32 & 48 & -40 & 0 & 0 \\
0 & -24 & -56 & 19 & 26 & 0 & 0 & 0 \\
-42 & 13 & 80 & -24 & -40 & 0 & 0 & 0 \\
-42 & 17 & 44 & -29 & 0 & 0 & 0 & 0 \\
18 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0
\end{bmatrix}$$
经过离散余弦逆变换后的矩阵 $M'$ 是:
$$\begin{bmatrix}
-65.83 & -62.63 & -71.04 & -68.04 & -55.65 & -64.99 & -68.37 & -45.72 \\
-70.87 & -72.59 & -72.07 & -45.82 & -20.30 & -40.63 & -65.74 & -57.11 \\
-70.40 & -78.12 & -68.13 & -17.40 & 19.72 & -14.45 & -60.84 & -63.38 \\
-63.00 & -73.21 & -61.78 & -7.56 & 26.97 & -13.59 & -60.21 & -57.75 \\
-58.02 & -65.09 & -61.36 & -27.06 & -6.29 & -40.45 & -67.70 & -50.14 \\
-57.26 & -57.09 & -64.34 & -57.62 & -48.02 & -65.58 & -72.36 & -47.25 \\
-53.45 & -45.52 & -60.89 & -73.60 & -64.55 & -63.43 & -62.21 & -44.67 \\
-47.14 & -34.38 & -53.26 & -73.78 & -60.19 & -47.06 & -46.88 & -40.80
\end{bmatrix}$$
经过加 $128$ 后并取整的矩阵是:
$$\begin{bmatrix}
62 & 65 & 57 & 60 & 72 & 63 & 60 & 82 \\
57 & 55 & 56 & 82 & 108 & 87 & 62 & 71 \\
58 & 50 & 60 & 111 & 148 & 114 & 67 & 65 \\
65 & 55 & 66 & 120 & 155 & 114 & 68 & 70 \\
70 & 63 & 67 & 101 & 122 & 88 & 60 & 78 \\
71 & 71 & 64 & 70 & 80 & 62 & 56 & 81 \\
75 & 82 & 67 & 54 & 63 & 65 & 66 & 83 \\
81 & 94 & 75 & 54 & 68 & 81 & 81 & 87
\end{bmatrix}$$
输入格式
从标准输入读入数据。
输入的前 $8$ 行,每行有空格分隔 $8$ 个正整数,是量化矩阵。
接下来的 $1$ 行是 $1$ 个正整数 $n$,表示扫描数据的个数。
接下来的 $1$ 行是 $1$ 个数字 $T$,取值为 $0$、$1$ 或 $2$,表示要进行的任务。
接下来的 $1$ 行,有空格分隔的 $n$ 个整数,是扫描数据。
输出格式
输出到标准输出。
输出共 $8$ 行,每行有 $8$ 个空格分隔的整数,表示一个图像矩阵。
当 $T$ 取 $0$ 时,输出填充(步骤 $3$)后的图像矩阵;当 $T$ 取 $1$ 时,输出量化(步骤 $4$)后的图像矩阵;当 $T$ 取 $2$ 时,输出最终的解码结果。
说明/提示
### 样例 1 解释
本组样例即为题目描述中的样例。
### 子任务
对于 $20\%$ 的数据,有 $T = 0$;
对于 $40\%$ 的数据,有 $T = 0$ 或 $1$;
对于 $40\%$ 的数据,有 $T \in \{0, 1, 2\}$,且 $n \in [0, 64]$,并且量化矩阵中的各个元素 $q_{i,j}$ 满足 $0 < q_{i,j} < 256$,扫描序列中的各个元素 $m_i$ 满足 $-256 < m_i < 256$。
### 提示
在 C/C++ 语言中,可以通过包含 `math.h`(C 语言)或 `cmath`(C++ 语言)来使用数学函数。$\pi$ 的值可以通过表达式 `acos(-1)` 获得。
在 Python 语言中,可以通过 `from math import pi` 引入 $\pi$。
在 Java 语言中,可以使用 `Math.PI` 来获取 $\pi$ 的值。