P13924 [POCamp 2024] 枝上雪栖 / Upplegå

> 圣诞之景，已然铺展，\ > 君之所行，处处皆欢。

只有当雪落在你家外面街道上所有 $N$ 棵树的树枝上时，才算是真正的冬天。街道上的所有树木可以用一个任意大的网格来表示。沿着街道，这 $N$ 棵树排成一排。每棵树 $i$ 的树干位于位置 $pos_i$，并由一个宽度为 1 的矩形描述，占据整个列 $pos_i$。此外，每棵树 $i$ 有 $s_i$ 根树枝。每根树枝都由一个高度为 1 的矩形描述，它从树干伸出，宽度为整数单位。保证每根树枝所占据的方格不包含任何其他树枝或树干。还保证没有树枝会延伸到另一棵树之外，甚至不会延伸到另一棵树之上。 在一个下雪的傍晚之后，Upplegå 已经覆盖了所有的树木。Upplegå 是瑞典语中指积聚在树枝上的雪。每根树枝的每个单位长度上都有 1 单位的雪。雪非常小，以至于它不占据一个方格。换句话说，高度可以忽略不计。 你是一个真正的冬季爱好者，热爱圣诞歌曲、舒适的寒冷天气，最重要的是，热爱所有的 Upplegå。根据天气预报，很快将有一场大风暴，会剧烈摇晃所有的树木。当一棵树被摇晃时，其树枝上的雪将开始垂直落下，直到雪安全地落在属于一棵未被摇晃的树的树枝上，或者落在地上。 尽管风暴即将来临，你仍有时间通过固定 $K$ 棵树来保护它们免受摇晃。由于你如此热爱雪，你希望计算通过精确固定 $K$ 棵树，可以防止多少单位的雪落到地面。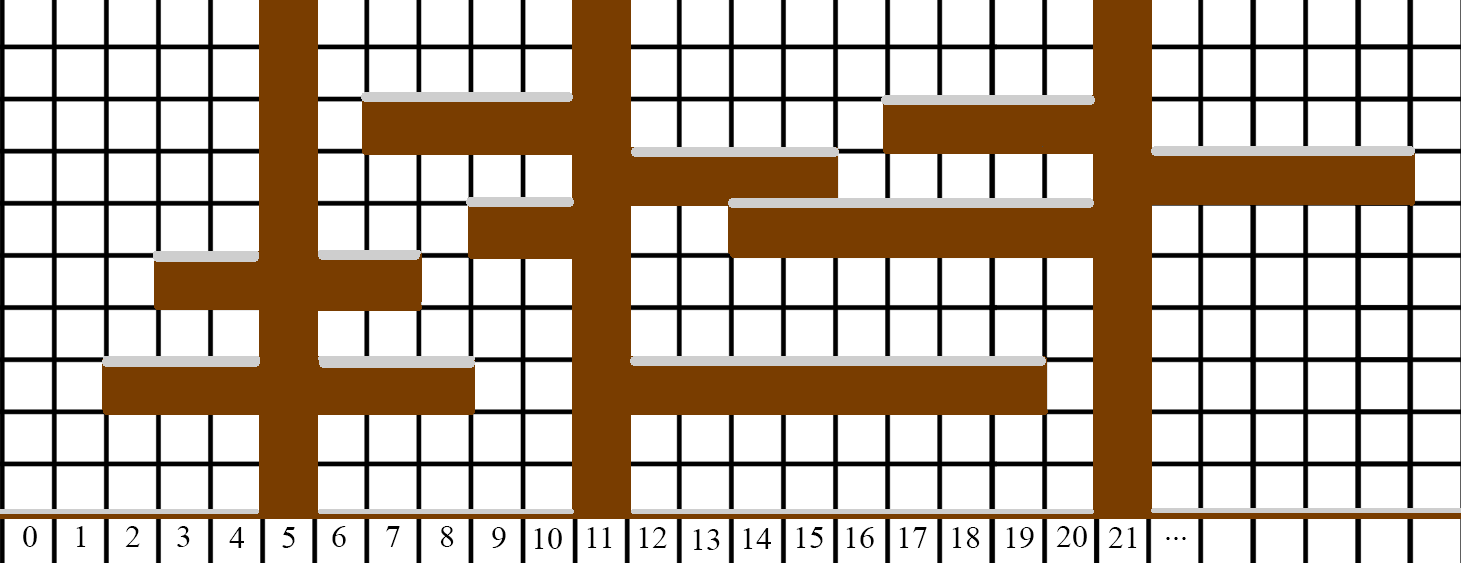  图 1：图片显示了示例 1。

输入的第一行包含两个整数 $N$ 和 $K$ ($1 \le K \le N \le 10^5$)，表示街道上的树木数量以及你有时间保护免受摇晃的树木数量。 第二行包含 $N$ 个整数 $pos_1, pos_2, \dots, pos_N$ ($0 \le pos_i \le 10^9$)，其中 $pos_i$ 是从街道起点到树 $i$ 的长度单位数。树木将按排序顺序给出，并且保证没有两棵树占据相同的位置。形式上，这意味着对于所有 $i < j$，都满足 $pos_i < pos_j$。 第三行包含 $N$ 个整数 $s_1, s_2, \dots, s_N$ ($1 \le s_i \le 10$)，其中 $s_i$ 是树 $i$ 上的树枝数量。 最后是 $2N$ 行，每棵树有 2 行，描述其树枝： * 第一行包含 $s_i$ 个整数 $h_{i,1}, h_{i,2}, \dots, h_{i,s_i}$ ($1 \le h_{i,j} \le 10^9$)，其中 $h_{i,j}$ 是属于树 $i$ 的第 $j$ 根树枝的高度。 * 第二行包含 $s_i$ 个整数 $l_{i,1}, l_{i,2}, \dots, l_{i,s_i}$ ($-10^9 \le l_{i,j} \le 10^9$, $l_{i,j} \neq 0$)。每个 $l_{i,j}$ 描述了树 $i$ 的第 $j$ 根树枝的长度和方向。如果 $l_{i,j}$ 为正，则表示第 $j$ 根树枝向右延伸，长度为 $l_{i,j}$ 单位。如果 $l_{i,j}$ 为负，则表示树枝向左延伸，长度为 $|l_{i,j}|$ 单位。 没有树枝会超出位于 0 的街道起点，或超出街道起点 $10^9$ 长度单位。

输出通过精确固定 $K$ 棵树，可以防止落到地面的最大雪单位数量。

### 样例解释 #### 样例 1 解释 通过选择拯救第一棵和第二棵树，我们阻止了 10 单位的雪从树 1 落下，18 单位的雪从树 2 落下，以及 9 单位的雪从树 3 落下，总计 $10 + 18 + 9 = 37$。 ### 子任务 **本题采用捆绑测试。** | 子任务编号 | 得分 | 限制 | |:-:|:-:|---| | $1$ | $5 $ | 所有分支都指向右侧。形式上，对于所有 $i, j$，都有 $l_{i,j} > 0$。 | | $2$ | $5 $ | $K = 1$ | | $3$ | $7 $ | $N \le 15$ | | $4$ | $11$ | $N \le 2000$，对于所有 $i, j$，都有 $\vert l_{i,j}\vert \le 2 \cdot 10^5, pos_i \le 2 \cdot 10^5$。 | | $5$ | $23$ | $N \le 2000$ | | $6$ | $31$ | 对于所有 $i, j$，都有 $\vert l_{i,j}\vert \le 2 \cdot 10^5, pos_i \le 2 \cdot 10^5$。 | | $7$ | $18$ | 无额外约束。 | 子任务 4 和 6 额外保证所有树木和分支的位置都在 0 到 $4 \cdot 10^5$ 之间。