P13952 [ICPC 2023 Nanjing R] Intersection over Union

$\textit{Intersection over Union}$, also known as the $\textit{Jaccard index}$ and the $\textit{Jaccard similarity}$ coefficient (originally given the French name coefficient de communauté by Paul Jaccard), is a statistic used for gauging the similarity and diversity of sample sets. The Jaccard coefficient measures similarity between finite sample sets, and is defined as the size of the intersection divided by the size of the union of the sample sets: $$J(A, B) = \frac{|A \cap B|}{|A \cup B|}$$ Intersection over Union (IOU) is also a widely used metric in computer vision for evaluating object detection and segmentation algorithms. A rectangle that is aligned with the x and y axes (i.e., its sides are parallel to the x and y axes) is often called an "axis-aligned rectangle", "axis-aligned bounding box" (AABB), or simply "bounding box". On the other hand, a rectangle that is not necessarily aligned with the x and y axes (i.e., its sides might be at an angle) is often called a "rotated rectangle", a "rotated bounding box", or an "oriented bounding box" (OBB). In computer vision and image processing applications, both types of rectangles are widely in use, depending on the problem at hand. In this problem, your task is to find an axis-aligned rectangle (AABB) that maximizes the IOU with a rotated rectangle (OBB). The IOU between two rectangles is defined as the area of the intersection between the two rectangles divided by the area of their union.

There are multiple test cases. The first line of the input contains an integer $T$ ($1 \le T \le 10^4$) indicating the number of test cases. For each test case: The first and only line contains eight integers $x_1$, $y_1$, $x_2$, $y_2$, $x_3$, $y_3$, $x_4$, $y_4$ ($-10^9 \le x_i, y_i \le 10^9$), where $(x_i, y_i)$ represents the coordinates of the $i$-th vertex of the rotated rectangle, in either clockwise or counterclockwise order. It's guaranteed that the rotated rectangle has a positive area.

For each test case, output one line containing one number indicating the maximum IOU between the rotated rectangle and the axis-aligned rectangle. Your answer will be considered correct if the absolute or relative error does not exceed $10^{-9}$.

The sample test cases are shown as follows. The input rectangles are shown with dots and the optimal axis-aligned rectangles are shown with hatching. :::align{center}  :::
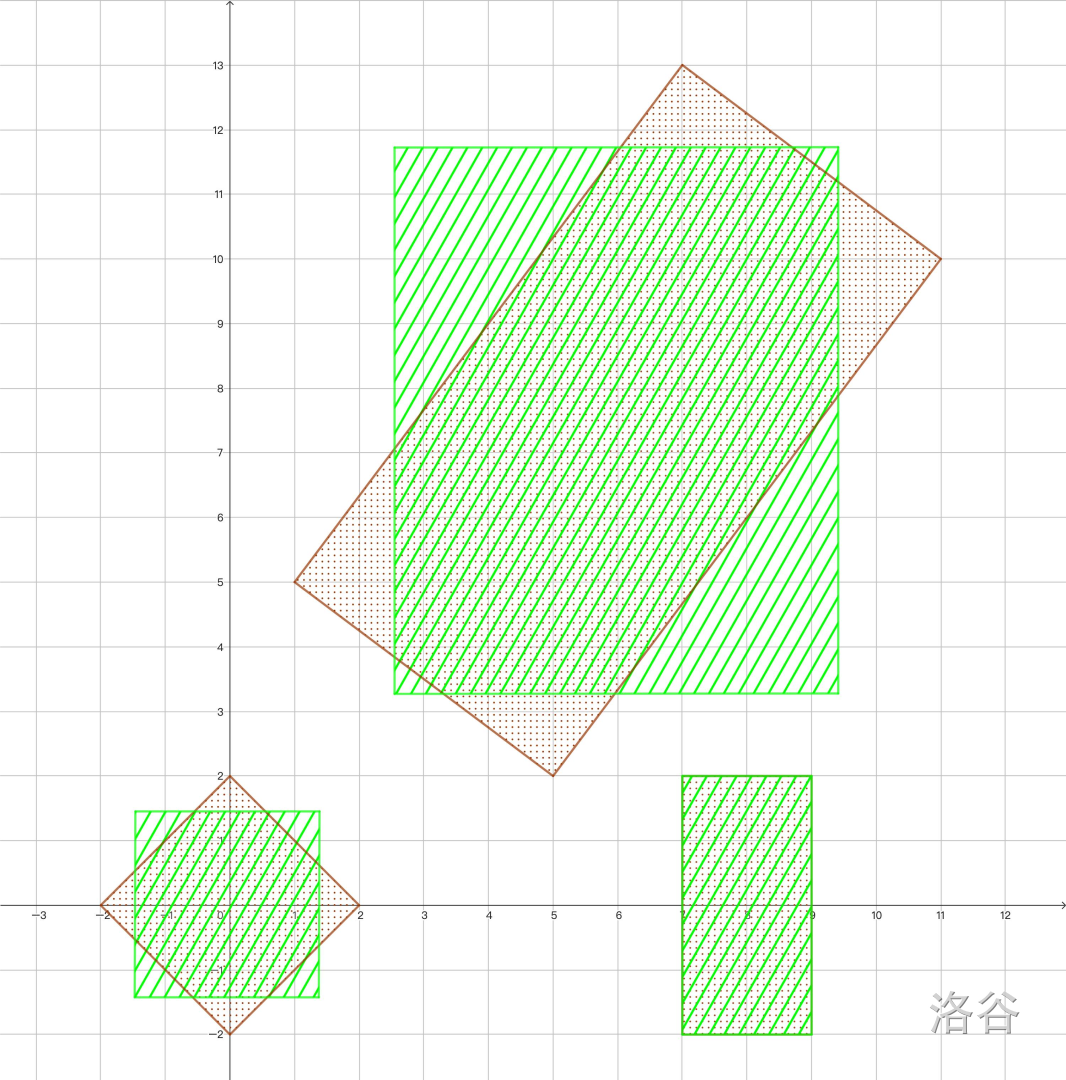