P13954 [ICPC 2023 Nanjing R] Red Black Tree

There is a rooted tree with $n$ vertices numbered from $1$ to $n$, where vertex $1$ is the root. Each vertex has a color, which is either red or black. We say a vertex is good, if every simple path from that vertex to any of its descendant leaf vertex contains the same number of black vertices. We say a tree is perfect, if all its vertices are good. Let $R_k$ be the subtree rooted at vertex $k$. For each $1 \le k \le n$, answer the following query: If you can choose a set of vertices and change their colors (that is, change red vertices to black, and change black vertices to red), calculate the minimum number of vertices you have to choose to make $R_k$ perfect. Recall that a simple path is a path which does not go through the same edge multiple times. Also recall that a subtree rooted at vertex $k$ is a tree consisting of all descendants of vertex $k$ and has vertex $k$ as the root. Note that any vertex is a descendant of itself.

There are multiple test cases. The first line of the input contains an integer $T$ indicating the number of test cases. For each test case: The first line contains an integer $n$ ($2 \le n \le 10^5$) indicating the number of vertices in the tree. The second line contains a string $s_1s_2\cdots s_n$ of length $n$ ($s_i \in \{0, 1\}$). If $s_i = 0$ then vertex $i$ is red; If $s_i = 1$ then vertex $i$ is black. The third line contains $(n - 1)$ integers $p_2, p_3, \cdots, p_n$ ($1 \le p_i < i$) where $p_i$ is the parent of vertex $i$. It's guaranteed that the sum of $n$ of all test cases will not exceed $10^6$.

For each test case output one line containing $n$ integers separated by a space, where the $i$-th integer indicates the minimum number of vertices whose color you have to change to make $R_i$ perfect. Please, DO NOT output extra spaces at the end of each line, or your solution may be considered incorrect!

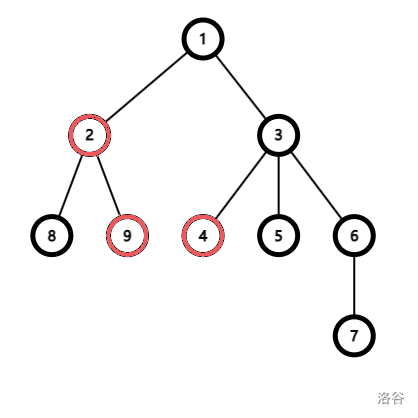
:::align{center}  ::: We illustrate the first sample test case. To make $R_1$ perfect, we can change the color of vertices $2$, $4$, $6$ and $9$. After that, all paths from vertex $1$ to its descendant leaves will contain $3$ black vertices, all paths from vertex $2$ to its descendant leaves will contain $2$ black vertices, and all paths from vertex $3$ to its descendant leaves will contain $2$ black vertices. As vertices $4$ to $9$ only has one descendant leaf, they're always good. To make $R_2$ perfect, we can change the color of vertex $8$. After that, all paths from vertex $2$ to its descendant leaves will contain $0$ vertices. As vertices $8$ and $9$ only has one descendant leaf, they're always good.