P13958 [ICPC 2023 Nanjing R] Puzzle: Question Mark

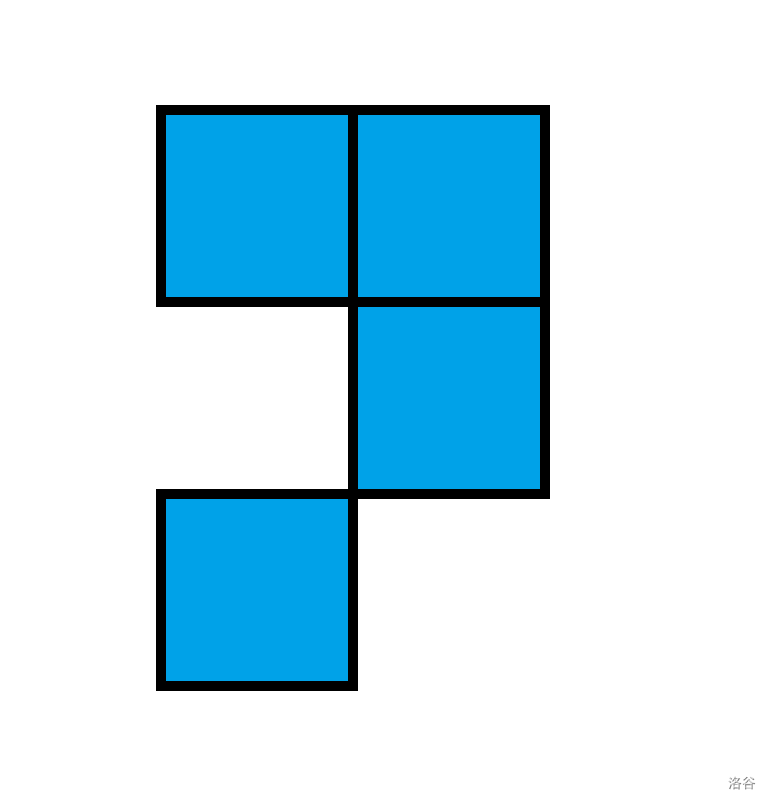
XingHui is a puzzle master. Today, she is playing a puzzle called $\textit{Filling with Question Marks}$. The puzzle contains a grid of $n$ rows and $n$ columns, and a handful of $\textit{question mark}$ pieces (QM pieces). A QM piece occupies $4$ cells, as shown in the following figure. :::align{center}  A QM piece (It looks like a question mark, I suppose?) ::: QM pieces must be placed entirely inside the grid and pieces can be rotated by a multiple of $90$ degrees and/or flipped. More precisely, there are $8$ types of QM pieces, as shown below. 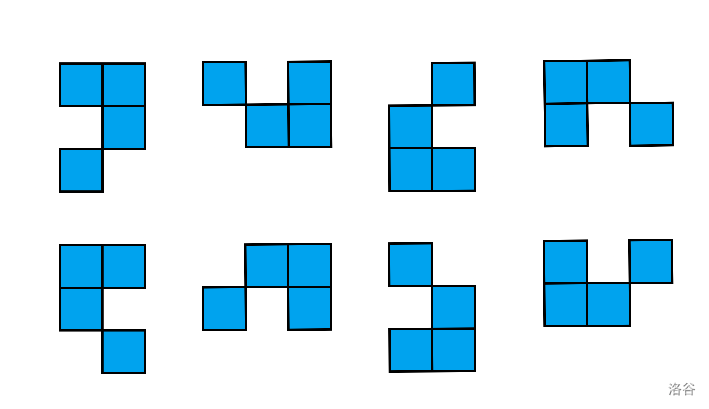:::align{center}  ::: Any two QM pieces cannot occupy the same cell. The goal of the puzzle is to find a way to place the maximum number of QM pieces on the $n \times n$ grid. XingHui wonders if you could solve the puzzle successfully.

There are multiple test cases. The first line of the input contains a single integer $T$ indicating the number of test cases. For each test case: The first and only line contains one integer $n$ ($1 \leq n \leq 2 \times 10^3$) indicating the size of the grid. It is guaranteed that the sum of $n^2$ of all test cases will not exceed $5 \times 10^6$.

For each test case: First output one line containing one integer indicating the maximum number of QM pieces placed on the grid. Then output $n$ lines. Each of these lines contains $n$ integers separated by a space. The $j$-th integer of the $i$-th line $a_{i,j}$ indicates that the cell on the $i$-th row and $j$-th column belongs to the $a_{i,j}$-th QM piece. If $a_{i,j}$ is $0$, it indicates that the corresponding cell is empty and does not belong to any QM piece. If there are multiple solutions, output any of them. Please, DO NOT output extra spaces at the end of each line, or your solution may be considered incorrect!

The sample test cases are shown below. :::align{center}   :::
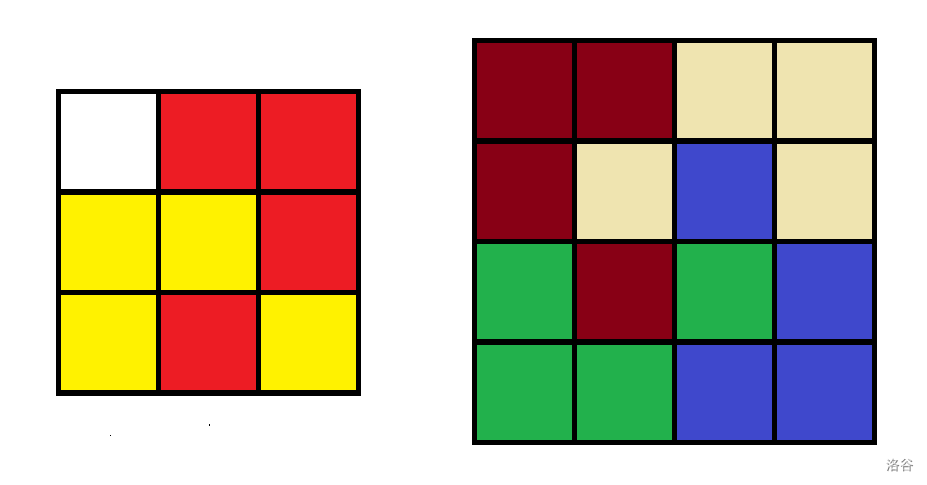