P13965 [VKOSHP 2024] Two-Story Advent Calendar

“General Passenger Company”正在推出从圣彼得堡到大乌斯秋格的新年列车游。为所有购买此行程的旅客，特别准备了一份礼物——一个降临节日历。 这个降临节日历的盒子形状像“General Passenger Company”的主力车型——一节双层火车车厢。盒子内部分为上下两层，每层都排列着若干小盒子，每个小盒子里都装有一颗糖果。上层有 $n$ 个小盒子，下层有 $m$ 个小盒子。每个小盒子上都标有一个从 $1$ 到 $n+m$ 的自然数，且这些数字互不重复。 每个小盒子的长度已知，不同盒子的长度可能不同。保证上下两层所有盒子的长度之和相等。 正确开启降临节日历的方法是：第 $1$ 天取出并打开编号为 $1$ 的盒子，第 $2$ 天取出并打开编号为 $2$ 的盒子，依此类推，最后一天取出并打开编号为 $n+m$ 的盒子。下图展示了一个降临节日历的示例。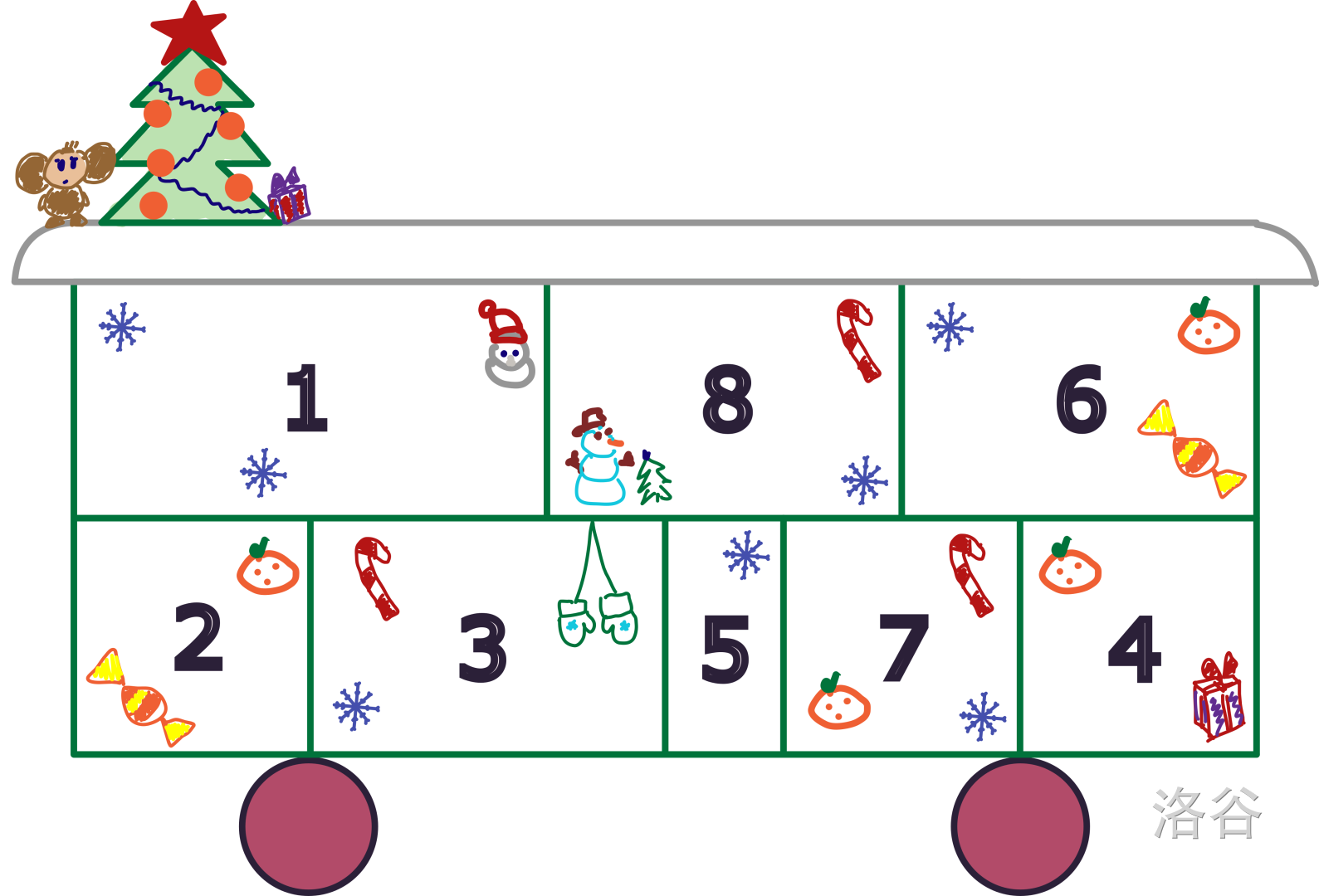 :::align{center}  有 $8$ 个格子的降临节日历。为了正确开启并营造新年氛围，你需要在新年前第 $8$ 天打开第 $1$ 个格子，在新年前第 $7$ 天打开第 $2$ 个格子，依此类推。最后一天——12 月 31 日——你需要打开第 $8$ 个格子。 ::: 设计师兼完美主义者 Maya 决定乘坐新年列车，并收到了一个双层降临节日历作为礼物。Maya 觉得，如果她在下层打开一个糖果盒时，上面正好还有未打开的上层盒子，这样很不方便。 Maya 很好奇，想知道她需要提前从日历中移除多少个盒子，才能让开启过程变得方便。同时，Maya 希望尽可能多地保留盒子。请你帮她计算，为了让每次打开下层盒子时，上面没有未打开的上层盒子，最少需要提前移除多少个盒子。可以从上层和下层任意移除盒子。

第一行输入一个整数 $n$（$1 \le n \le 10^{5}$），表示日历上层的盒子数量。 接下来 $n$ 行，每行包含两个整数 $a_i$ 和 $x_i$（$1 \le a_i \le 10^{9}$，$1 \le x_i \le n + m$），分别表示上层第 $i$ 个盒子的长度和编号。 第 $n+1$ 行输入一个整数 $m$（$1 \le m \le 10^{5}$），表示日历下层的盒子数量。 接下来 $m$ 行，每行包含两个整数 $b_j$ 和 $y_j$（$1 \le b_j \le 10^{9}$，$1 \le y_j \le n + m$），分别表示下层第 $j$ 个盒子的长度和编号。 保证 $a_1 + a_2 + \ldots + a_n = b_1 + b_2 + \ldots + b_m$。 保证集合 $\{x_1, x_2, \ldots, x_n, y_1, y_2, \ldots, y_m\}$ 中的所有数字互不相同。

输出一个整数 $k$，表示为使日历开启过程方便，最少需要提前移除的盒子数量。

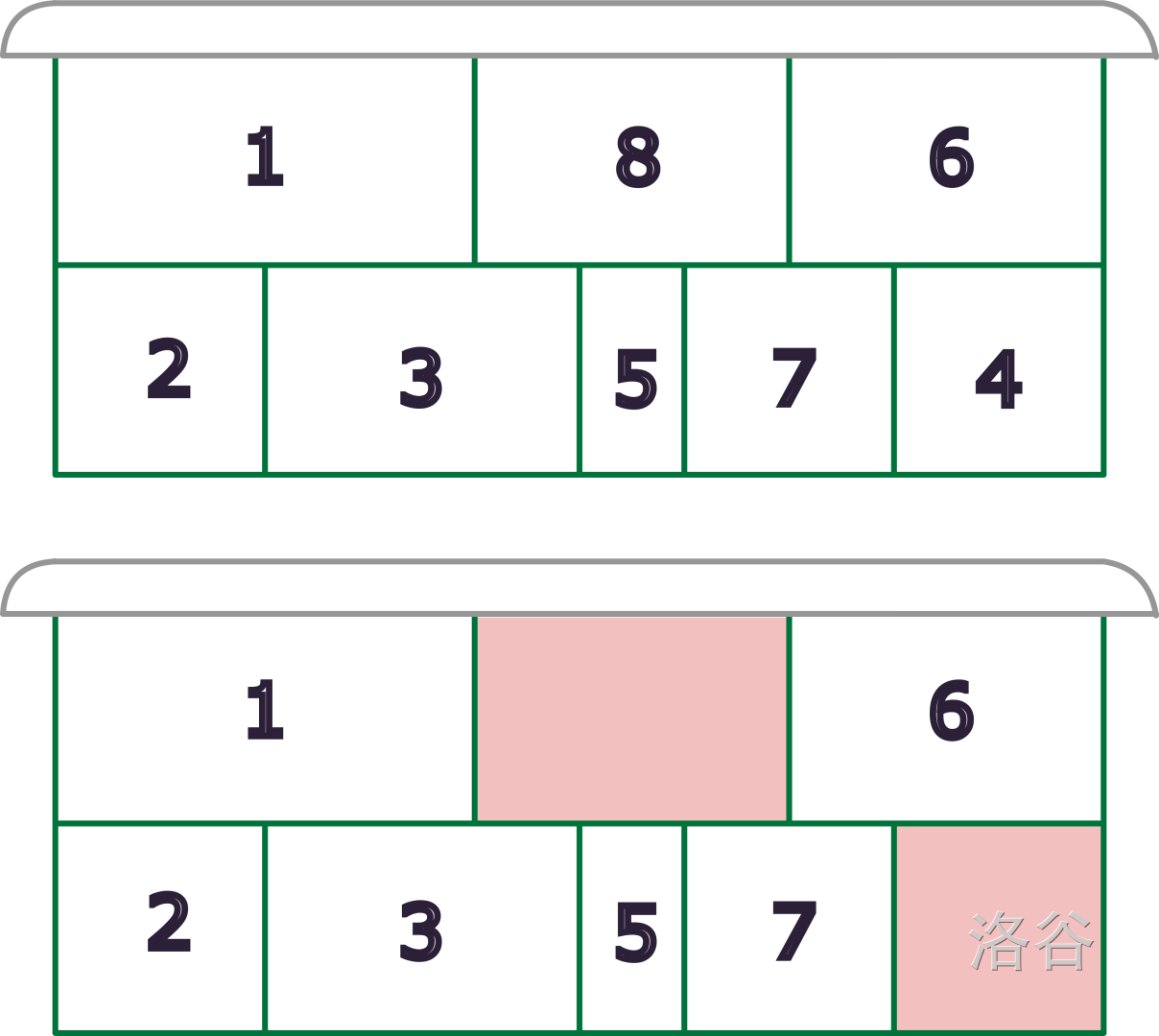
在第二个样例中，你可以移除编号为 $4$ 和 $8$ 的盒子。此后，日历将如下面所示，并变得方便。 :::align{center}  ::: 由 ChatGPT 4.1 翻译