P13966 [VKOSHP 2024] Intermediate Verticality

Two classical graph algorithms --- depth-first search and breadth-first search --- construct two spanning trees in a graph. The depth-first search is known for producing a tree that has no $\textit{horizontal}$ edges, which are edges connecting vertices that are not ancestors of each other, while breadth-first search is known for producing a tree that has no $\textit{vertical}$ edges --- edges connecting a vertex to its ancestor in the tree. In this problem, you will need to construct an intermediate spanning tree that has a specified number of horizontal and vertical edges. Recall that an undirected graph consists of a set of vertices $V$ and a set of edges $E$, where each edge connects two vertices. We will consider connected graphs, where it is possible to reach any vertex from any other vertex via edges. A tree is a connected undirected graph that contains no cycles, and a spanning tree in a graph is a subset of its edges that forms a tree, allowing one to reach any vertex of the graph from any other. Recall two fundamental properties of a tree: in a tree with $n$ vertices, there are exactly $n-1$ edges, and there is exactly one path between any two vertices in a tree. We will designate a vertex $r$ in the graph, which we will call the $\textit{root}$ of the tree. The vertices that lie on the unique path from vertex $x$ to vertex $r$ are called the $\textit{ancestors}$ of vertex $x$, and the first vertex on this path is called the $\textit{parent}$ of vertex $x$ and is denoted as $p_x$. The root has no parent. If a root and a spanning tree are fixed in the graph, then all edges of the graph can be divided into three types: - $\textit{tree edges}$ --- the edges of the chosen spanning tree; - $\textit{vertical edges}$ --- the edges not belonging to the tree that connect a vertex to its ancestor; - $\textit{horizontal edges}$ --- the remaining edges of the graph. 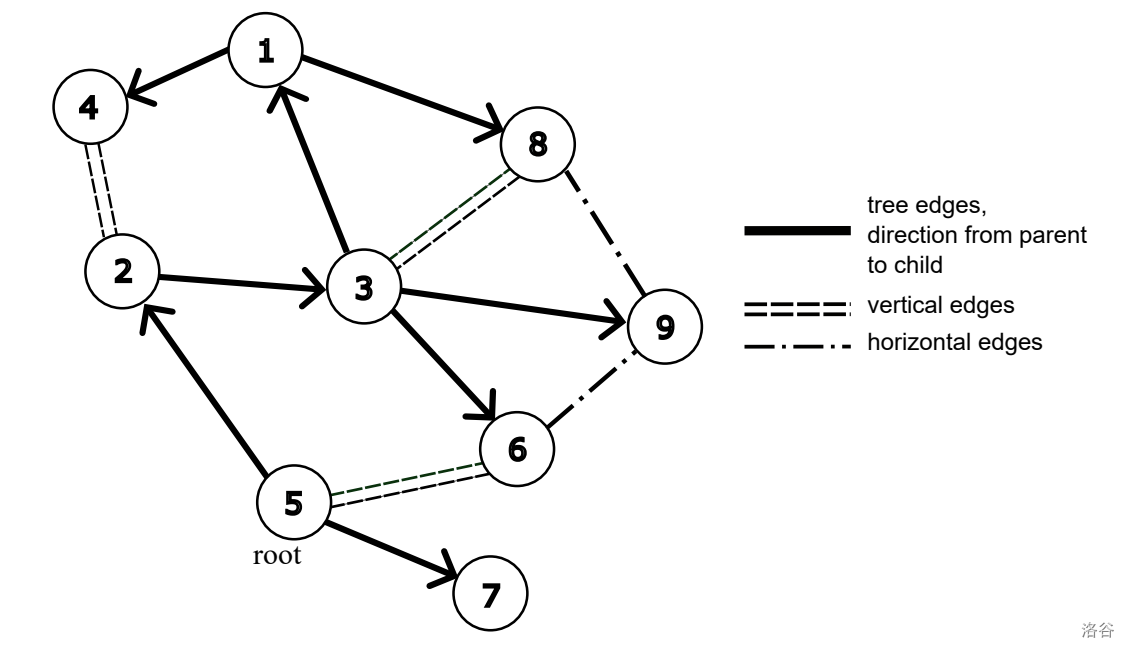:::align{center}  ::: The $\textit{verticality}$ of the spanning tree in the graph is defined as the number of vertical edges. You are given a graph with $n$ vertices and $m$ edges, the root of the tree $r$, and a number $h$, $0 \le h \le m-n+1$. You need to construct a spanning tree of the given graph with root at $r$, having a verticality equal to $h$, or report that such a tree does not exist.

Each test consists of several sets of input data. The first line contains one integer $t$ --- the number of sets of input data ($1 \le t \le 10^5$). Following this are descriptions of $t$ sets of input data. In the first line of each set of input data, there are four integers $n$, $m$, $r$, and $h$ --- the number of vertices and edges in the graph, respectively, the index of the root vertex, and the required verticality of the future spanning tree ($2 \le n \le 3 \cdot 10^5$; $n - 1 \le m \le 3 \cdot 10^5$; $1 \le r \le n$; $0 \le h \le m - n + 1$). In each of the following $m$ lines, there are two integers $u_i$, $v_i$ --- the indices of the vertices connected by an edge in the graph ($1 \le u_i, v_i \le n$; $u_i \ne v_i$). It is guaranteed that all graphs are connected, contain no loops or multiple edges. It is guaranteed that the sum of $n$ across all input data sets does not exceed $3 \cdot 10^5$. It is guaranteed that the sum of $m$ across all input data sets does not exceed $3 \cdot 10^5$.

For each test case, find the required spanning tree $T$ and output in a separate line $n$ integers $p_1, p_2, \ldots, p_n$, where $p_i$ is the index of the parent of the $i$-th vertex in the tree $T$ ($1 \le p_i \le n$). For $p_r$, you can output any number from $1$ to $n$. If a tree $T$ with the desired properties does not exist, output $n$ numbers $-1$ instead.