P13973 [VKOSHP 2024] Nightmare Sum

Given an array $a$ of length $n$, consisting of distinct positive integers. Compute $$\sum\limits_{l=1}^{n} \sum\limits_{r=l}^{n} \left\lfloor\frac{\max(a_{l},a_{l+1},\ldots,a_{r})}{\min(a_{l},a_{l+1},\ldots,a_{r})}\right\rfloor$$ Here, $\lfloor x \rfloor$ denotes $x$ rounded down to the nearest integer. Thus, it is necessary to compute the sum of the results of integer division of the maximum by the minimum over all subarrays of the array $a$.

The first line of input contains a single integer $n$~--- the length of the array $(1 \leq n \leq 300\,000)$. The second line of input contains $n$ integers~--- the array $a$ $(1 \leq a_{i} \leq 300\,000)$. It is guaranteed that all numbers in the array $a$ are distinct.

Output a single number --- the desired sum.

Let's consider the example in more detail: :::align{center}  :::
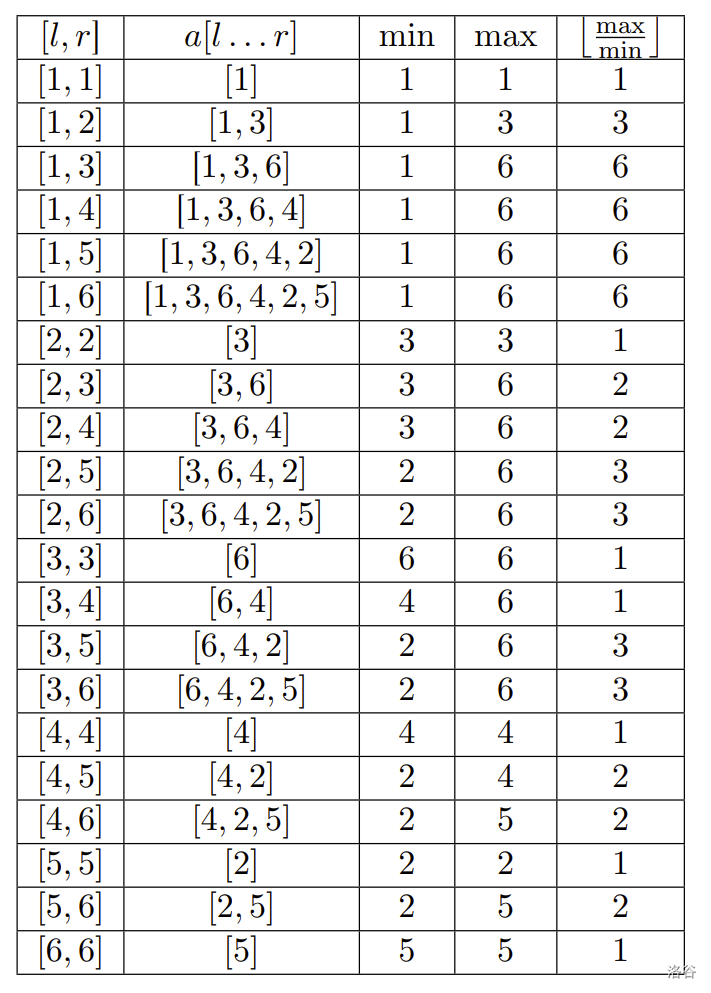