P13987 [PO Final 2023] 修桥 / Bridge Building

1s, 2G, brobygge2

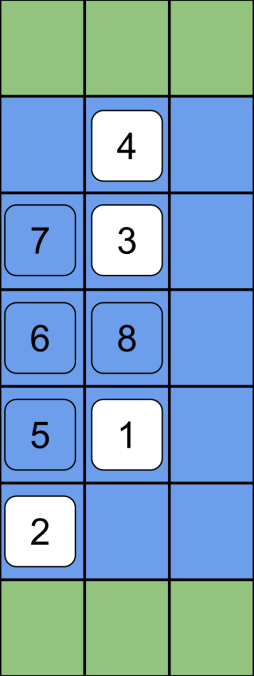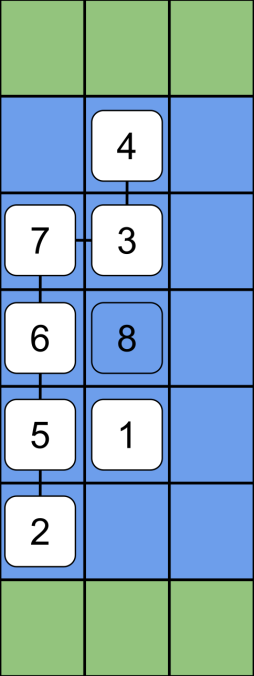
不会游泳的 Rut 想要穿过一条河。幸运的是，河流的一段正在修建桥梁，这一段可以表示为一张 $ N \times M $ 的网格。每经过 1 小时，就会在一块原本被水覆盖的格子上建成一段桥面。例如，经过 5 小时将建成 5 段桥面。Rut 已经拿到了最先建成的桥面位置列表。她知道：当她能够在不需要游泳的情况下，沿着桥从河的一侧走到另一侧时，就可以过河。她从第 $ 0 $ 行出发，目标是到达第 $ N - 1 $ 行。这两行上各有一整条可供沿河行走的陆地。她可以在不被水覆盖的格子之间，上下、下上、左右移动。现在她想知道：给定的这些桥段是否足以让她过河；如果可以，她最少需要等待多少小时，才能在桥面足够完成时到达对岸。   图 1：样例 $1$ 在 $4$ 小时和 $7$ 小时后的示意图。只有在 $7$ 小时后才会出现通往对岸的路径。

输入的第一行包含三个整数 $ N, M $（$ 3 \le N, M \le 10^9 $）和 $ T $（$ 1 \le T \le 10^5 $），分别表示网格的行数、列数以及将要建成的桥段数。 接下来有 $ T $ 行，其中第 $ i $ 行包含两个整数 $ R $（$ 1 \le R \le N - 2 $）和 $ C $（$ 0 \le C \le M - 1 $），表示第 $ i $ 小时完成的格子的行与列。注意：本题中，第 $ 0 $ 行是底部行。

如果 Rut 能过河，输出一个整数：Rut 至少需要等待的小时数，使得桥面足以通往对岸；否则，输出 $\texttt{nej}$（瑞典语「No」）。

### 子任务 **本题采用捆绑测试。** | 子任务编号 | 分值 | 限制 | |:-:|:-:|-------------| | $1$ | $10$ | $ N \le 4 $ | | $2$ | $20$ | $ N, M \le 50 $ | | $3$ | $30$ | $ N, M \le 1000 $ | | $4$ | $15$ | $ T \le 2000 $ | | $5$ | $25$ | 无额外限制。 |