P1398 [NOI2013] Calligrapher

Student Xiao E loves calligraphy. He heard that NOI2013 has started, and he wants to write the word "NOI" to give to everyone. Xiao E has a magical sheet of paper, which can be represented as a 2D grid of $n$ rows and $m$ columns. For convenience, we define the lower-left cell of the grid to have coordinates $(1, 1)$, and the upper-right cell to have coordinates $(m, n)$. Each cell in the grid has an integer luck value. Writing on the cells increases everyone’s luck. The total luck equals the sum of the luck values of all the cells touched by the brush. Now you need to write the three letters `N`, `O`, and `I` on the paper. Definitions of the three calligraphic letters: - `N` consists of several (at least $3$) rectangles whose edges are parallel to the coordinate axes. Suppose it consists of $K$ rectangles (indexed $1 \ldots K$). Let the lower-left cell of the $i$-th rectangle be $(L_i, B_i)$ and the upper-right cell be $(R_i, T_i)$. They must satisfy: 1. $L_i \le R_i, B_i \le T_i$. 2. For any $1 < i \le K$, $L_i = R_{i-1} + 1$. 3. For any $3 \le i < K$, $B_{i-1} - 1 \le T_i \le T_{i-1}$, $B_i \le B_{i-1}$. 4. $B_2 > B_1$, $T_2 = T_1$, $B_{K-1} = B_K$, $T_{K-1} < T_K$. - `O` is formed by taking a large rectangle $A$ and removing a smaller rectangle $B$ from its interior. Both rectangles are axis-aligned. Let the lower-left cell of the large rectangle $A$ be $(u, v)$, with width $W$ and height $H$. Then the small rectangle $B$ has lower-left cell $(u + 1, v + 1)$, width $W - 2$, and height $H - 2$. They must satisfy: 1. $W \ge 3$, $H \ge 3$. 2. $u > R_K + 1$. - `I` consists of $3$ solid rectangles whose edges are parallel to the coordinate axes and are stacked from bottom to top, indexed $1, 2, 3$ from bottom to top. Let the lower-left cell of the $i$-th rectangle be $(P_i, Q_i)$ and the upper-right cell be $(G_i, H_i)$. They must satisfy: 1. $P_i \le G_i, Q_i \le H_i$. 2. $P_1 = P_3 > u + W$, $G_1 = G_3$. 3. $Q_1 = H_1 = Q_2 - 1$, $H_2 + 1 = Q_3 = H_3$. 4. $P_1 < P_2 \le G_2 < G_1$. 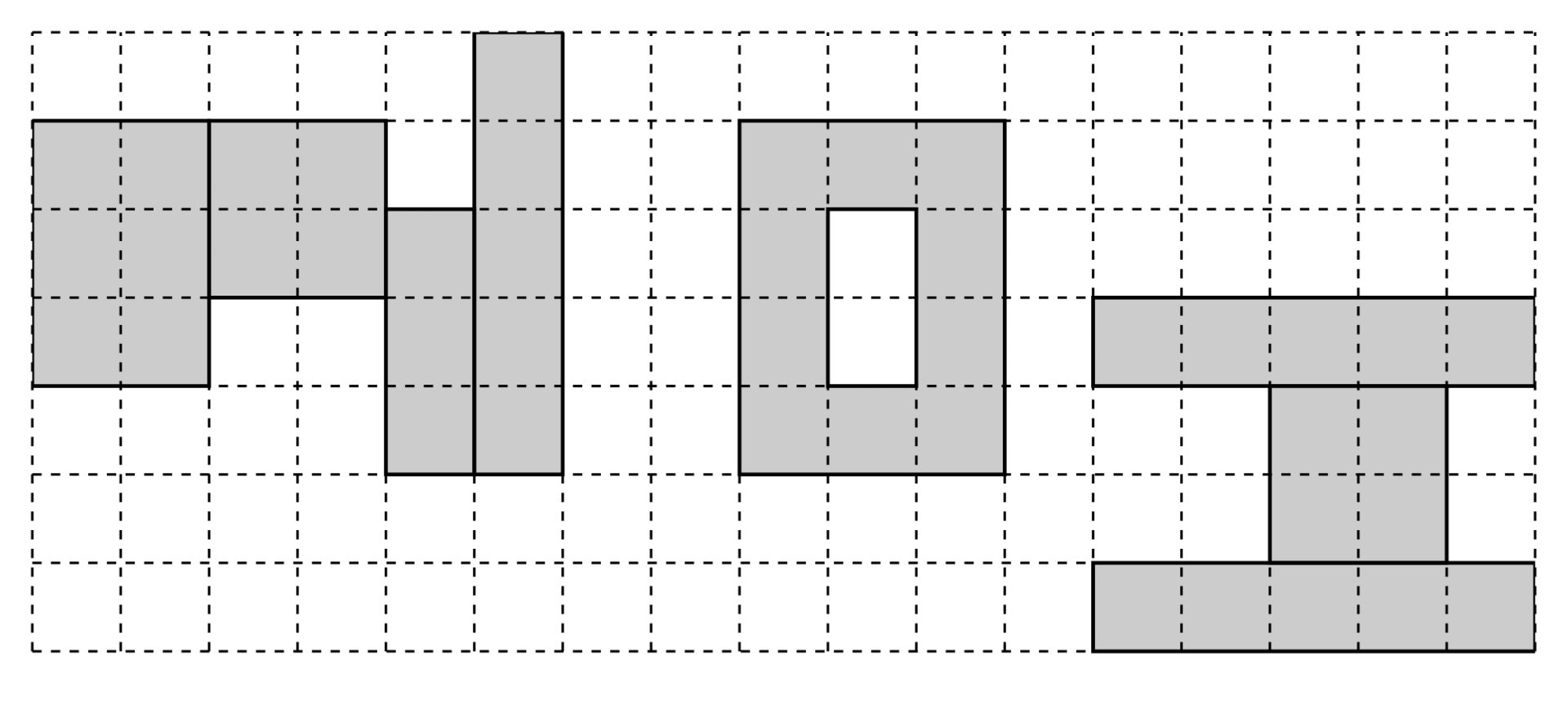An example of `N`, `O`, and `I` is shown below:  In addition, all drawn shapes are not allowed to go beyond the boundaries of the paper. Now Xiao E wants to know the maximum total luck he can achieve.

The first line contains two positive integers $n$ and $m$, representing the number of rows and columns of the matrix, respectively. Then $n$ lines follow, each containing $m$ integers. In the $(i + 1)$-th line, the $j$-th number is the luck value of cell $(j, n - i + 1)$.

Output an integer $T$, which is the maximum total luck that Xiao E can obtain.

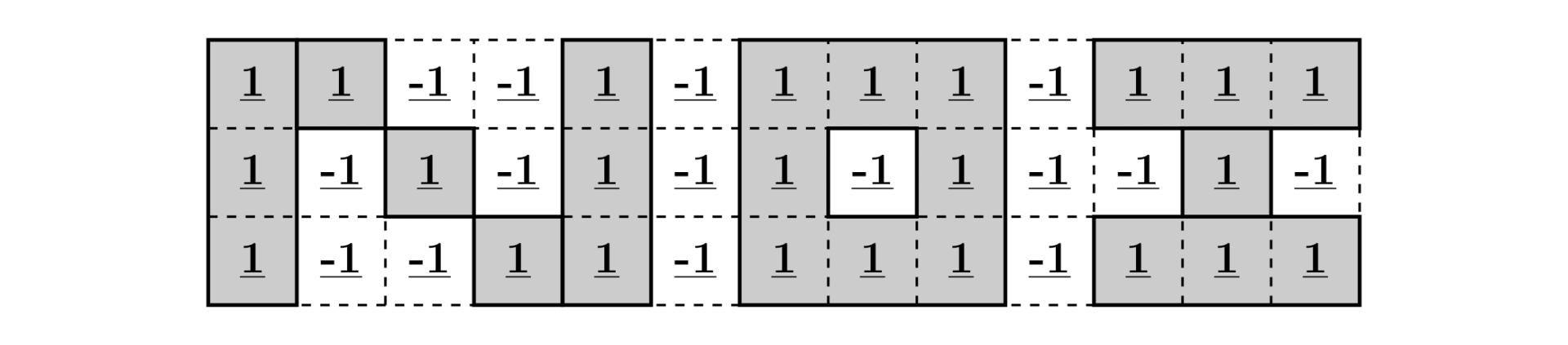
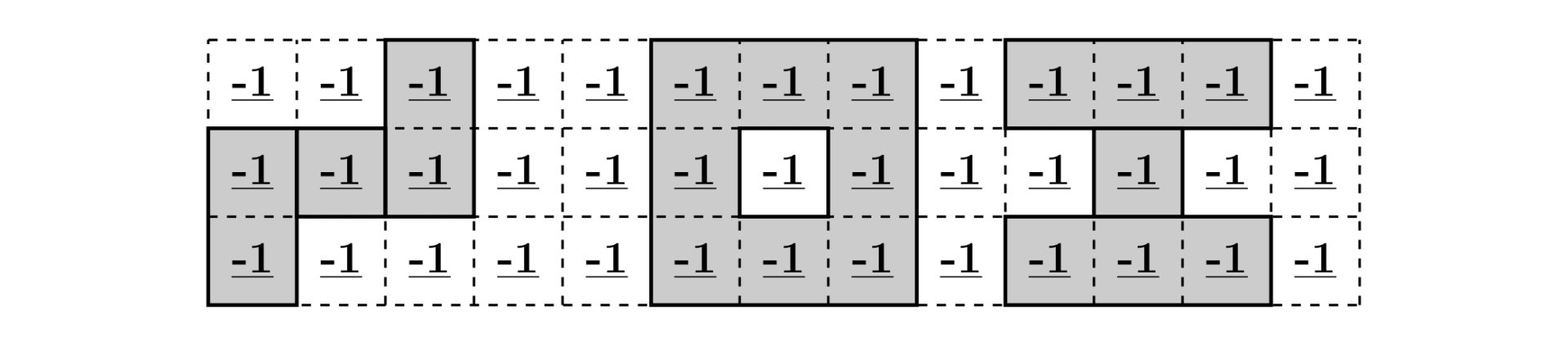
### Sample Explanation 1  ### Sample Explanation 2  ### Constraints | Test point ID | $n$ | $m$ | Luck value range | | :-----------: | :-----: | :------: | :--------------: | | 1 | $=3$ | $=12$ | $[-50,50]$ | | 2 | ^ | ^ | ^ | | 3 | ^ | ^ | ^ | | 4 | ^ | ^ | ^ | | 5 | $\le10$ | $\le20$ | ^ | | 6 | ^ | ^ | ^ | | 7 | ^ | ^ | ^ | | 8 | ^ | ^ | ^ | | 9 | $\le150$| $\le500$ | $=1$ | | 10 | ^ | ^ | ^ | | 11 | $\le80$| $\le80$ | $[-200,200]$ | | 12 | ^ | ^ | ^ | | 13 | ^ | ^ | ^ | | 14 | ^ | ^ | ^ | | 15 | $\le150$| $\le500$ | ^ | | 16 | ^ | ^ | ^ | | 17 | ^ | ^ | ^ | | 18 | ^ | ^ | ^ | | 19 | ^ | ^ | ^ | | 20 | ^ | ^ | ^ | For all testdata, it is guaranteed that $n \ge 3, m \ge 12$. Translated by ChatGPT 5