P13999 [eJOI 2025] Collecting Diamonds

在罗多彼山脉发现了一处钻石矿床。为方便起见，设该矿床有 $N$ 个大厅，编号为 $0$ 到 $N-1$。有 $M$ 条单向走廊连接着若干大厅，并且 **每个** 大厅至少有一条走廊从它出发。每条走廊在通过时都能开采到一定数量的钻石。这个数量在多次通过时 **不会变化**——也就是说，重复通过该走廊，收集到的钻石数保持不变。 可能存在一条走廊把某个大厅连到自身；同一对大厅之间也可能存在多条走廊（包括方向相同的多条）。此外，也 **不保证** 所有大厅两两可达：即可能存在一对大厅 $(x, y)$，使得无法从 $x$ 到达 $y$。 Petar 将恰好通过 $K$ 条走廊来采集钻石。他会先选择某个大厅 $s$ 作为起点，然后沿一条从 $s$ 出发的走廊移动到下一个大厅，如此反复，直到恰好通过了 $K$ 条走廊为止。注意，他可以重复进入大厅与走廊；并且每次经过同一条走廊，收集到的钻石数量都不会改变。还要注意，总能找到一条可以连续通过 $K$ 条走廊的途径。 Petar 选择起点 $s$ 与行走路径的方式如下：首先，他希望 **第一** 条经过的走廊所获得的钻石数最大；在所有能使第一条走廊钻石数最大的方案中，他再选择 **第二** 条走廊钻石数最大的方案；以此类推，共进行 $K$ 次。换言之，Petar 想要选择 **字典序最大** 的走廊序列。他想知道在这种策略下，自己最终能收集到多少钻石。请帮助他计算这一总数。 ### 实现细节 你需要实现函数 `calculate_diamonds`： ```cpp long long int calculate_diamonds(int N, int M, int K, std::vector u, std::vector v, std::vector d) ``` - $N$：矿床中的大厅数； - $M$：大厅之间的走廊数； - $K$：Petar 将要经过的走廊数； - $u$、$v$、$d$：长度为 $M$ 的整数向量，分别表示每条走廊的起点大厅、终点大厅以及该走廊可采的钻石数。 该函数在每个测试中被调用一次，并返回一个数——Petar 采用上述策略时能收集到的钻石总数。

输入格式如下： - 第 $1$ 行：三个整数——$N$、$M$、$K$。 - 第 $1 + i$ 行：三个整数 $u[i]$、$v[i]$、$d[i]$——表示一条从大厅 $u[i]$ 出发、到达大厅 $v[i]$ 的走廊，可采钻石为 $d[i]$。

输出格式如下： - 第 $1$ 行：一个整数——函数调用的返回值。

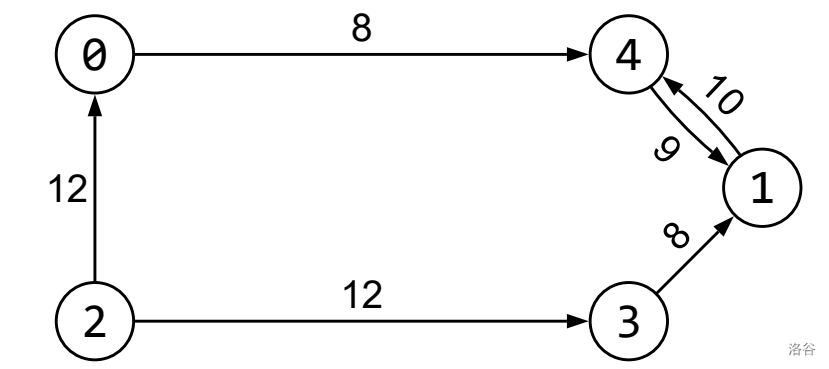
### 示例 1 考虑如下调用与示意图，$N = 5, M = 6, K = 4$： ``` calculate_diamonds(5, 6, 4, {2, 0, 4, 2, 3, 1}, {0, 4, 1, 3, 1, 4}, {12, 8, 9, 12, 8, 10}) ``` :::align{center}  ::: Petar 会选择经过如下走廊：$2 \overset{12}{\rightarrow} 3 \overset{8}{\rightarrow} 1 \overset{10}{\rightarrow} 4 \overset{9}{\rightarrow} 1$。他收集到的总钻石数为 $39$，这也是函数应返回的值。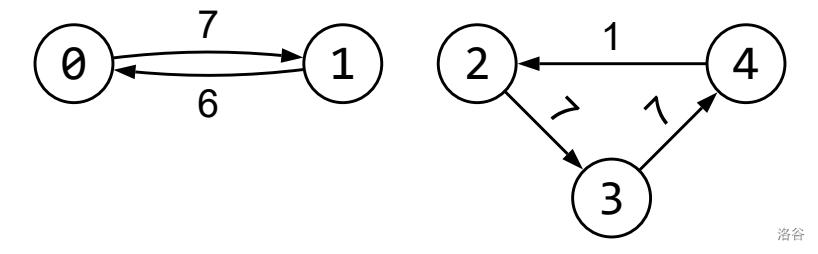 ### 示例 2 考虑如下调用与示意图，$N = 5, M = 5, K = 4$： ``` calculate_diamonds(5, 5, 4, {0, 1, 2, 3, 4}, {1, 0, 3, 4, 2}, {7, 6, 7, 7, 1}) ``` :::align{center}  ::: 共有 $5$ 种经过 $4$ 条走廊的选择： (1) $0 \overset{7}{\rightarrow} 1 \overset{6}{\rightarrow} 0 \overset{7}{\rightarrow} 1 \overset{6}{\rightarrow} 0$； (2) $1 \overset{6}{\rightarrow} 0 \overset{7}{\rightarrow} 1 \overset{6}{\rightarrow} 0 \overset{7}{\rightarrow} 1$； (3) $2 \overset{7}{\rightarrow} 3 \overset{7}{\rightarrow} 4 \overset{1}{\rightarrow} 2 \overset{7}{\rightarrow} 3$； (4) $3 \overset{7}{\rightarrow} 4 \overset{1}{\rightarrow} 2 \overset{7}{\rightarrow} 3 \overset{7}{\rightarrow} 4$； (5) $4 \overset{1}{\rightarrow} 2 \overset{7}{\rightarrow} 3 \overset{7}{\rightarrow} 4 \overset{1}{\rightarrow} 2$。 方案 (2) 与 (5) 不能使第一条走廊的钻石数最大；在方案 (1)、(3)、(4) 中，只有方案 (3) 能使 **第二** 条走廊的钻石数最大，因此它是 Petar 的最佳选择。注意，方案 (3) 并 **不** 使 **第三** 条走廊的钻石数最大，也 **不** 使总钻石数最大，但它是 **唯一的字典序最大** 序列。Petar 收集到的总钻石数为 $22$，这也是函数应返回的值。 ### 约束 - $1 \leq N \leq 2000$ - $1 \leq M \leq 4000$ - $1 \leq K \leq 10^9$ - $0 \leq u[i], v[i] < N$ - 对每个 $0 \leq i < M$，$1 \leq d[i] \leq 10^9$ - 保证每个大厅至少有一条走廊从其出发。 - **注意：内存限制异常之小，仅为 4 MB。** ### 子任务 | Subtask | Points | Required subtasks | $N$ | $M$ | $K$ | Additional constraints | | :-: | :-: | :-: | :-: | :-: | :-: | :-: | | 0 | $0$ | - | - | - | - | The examples. | | 1 | $11$ | $0$ | $\leq 10$ | $\leq 20$ | $\leq 10$ | - | | 2 | $10$ | $0-1$ | $\leq 100$ | $\leq 1000$ | $\leq 1000$ | - | | 3 | $26$ | $0-2$ | $\leq 100$ | $\leq 1000$ | $\leq 10^9$ | - | | 4 | $11$ | - | $\leq 2000$ | $=N$ | $\leq 10^9$ | 每个大厅恰有一条走廊从其出发，且恰有一条走廊以其为终点。 | | 5 | $10$ | - | $\leq 2000$ | $\leq 4000$ | $\leq 10^9$ | 所有 $d[i]$ 互不相同。 | | 6 | $11$ | - | $\leq 2000$ | $\leq 4000$ | $\leq 10^9$ | 存在且仅存在一个 $d[i] = 2$（$0 \leq i < M$），其余 $d$ 值均为 $1$。 | | 7 | $21$ | $0-6$ | $\leq 2000$ | $\leq 4000$ | $\leq 10^9$ | - | 翻译由 ChatGPT-5 完成。