P13999 [eJOI 2025] Collecting Diamonds

A diamond deposit has been discovered in the Rhodope Mountains. For simplicity, we will assume that the deposit has $N$ halls, labeled with integers from $0$ to $N-1$. There are $M$ one-way corridors connecting some of the halls such that there is at least one corridor going out of each hall. Each corridor has a certain number of diamonds that can be mined when passing through it. This number **does not change** when passing through the corridor – it remains the same for subsequent passes. It is possible that a corridor connects a hall to itself, and there may be multiple corridors between the same pair of halls (possibly in the same direction). It is also not guaranteed that the halls are connected; i.e., there may be a pair of halls $(x, y)$ such that $y$ cannot be reached from $x$. Petar will pass through $K$ corridors to mine diamonds. He will choose some hall $s$ to begin with, then move to a hall by passing through a corridor starting from $s$, and so on until he has passed through exactly $K$ corridors. Note that he can repeat halls and corridors, and that the number of diamonds he collects from a corridor does not change upon repetition. Notice that there is always going to be a way for him to pass through $K$ corridors consecutively. Petar will choose $s$ and the path he will follow in the following way: First, he wants to maximize the number of diamonds he will collect from the first corridor he passes through. Among all such options, he will choose the one that maximizes the number of diamonds he will collect from the second corridor. This repeats $K$ times. In other words, Petar wants to choose a lexicographically greatest path. He wonders what the total number of diamonds he will collect is if he chooses such a path. Help him calculate this. ### Implementation details You should implement the function `calculate_diamonds`: ```cpp long long int calculate_diamonds(int N, int M, int K, std::vector u, std::vector v, std::vector d) ``` - $N$: the number of halls in the diamond deposit; - $M$: the number of corridors between the halls; - $K$: the number of corridors Petar will pass; - $u$, $v$, $d$: vectors of $M$ integers, representing the starting halls, ending halls, and diamonds for the corridors. This function will be called once for each test and has to return one number – the total number of diamonds Petar will collect using his strategy.

The input format is the following: - line 1: three integers – the values of $N$, $M$, and $K$. - line $1 + i$: three integers $u[i]$, $v[i]$, $d[i]$ – representing a corridor starting from hall $u[i]$ and ending in hall $v[i]$ with $d[i]$ diamonds for mining.

The output format is the following: - line 1: one integer – the return value of the call.

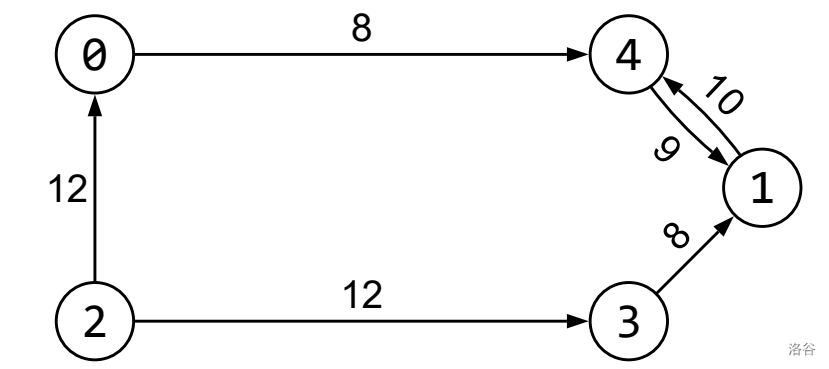
### Example 1 Consider the following call and illustration, for $N=5,M=6$ and $K=4$: ``` calculate_diamonds(5, 6, 4, {2, 0, 4, 2, 3, 1}, {0, 4, 1, 3, 1, 4}, {12, 8, 9, 12, 8, 10}) ``` :::align{center}  ::: Petar will choose to pass through the following corridors: $2 \overset{12}{\rightarrow} 3 \overset{8}{\rightarrow} 1 \overset{10}{\rightarrow} 4 \overset{9}{\rightarrow} 1$. The total number of diamonds he will collect is 39, which should be the value returned by the call. 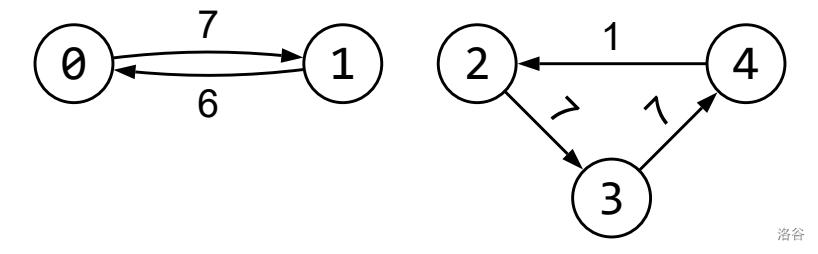### Example 2 Consider the following call and illustration, for $N=5,M=5$ and $K=4$: ``` calculate_diamonds(5, 5, 4, {0, 1, 2, 3, 4}, {1, 0, 3, 4, 2}, {7, 6, 7, 7, 1}) ``` :::align{center}  ::: There are 5 options for passing through 4 corridors: (1) $0 \overset{7}{\rightarrow} 1 \overset{6}{\rightarrow} 0 \overset{7}{\rightarrow} 1 \overset{6}{\rightarrow} 0$; (2) $1 \overset{6}{\rightarrow} 0 \overset{7}{\rightarrow} 1 \overset{6}{\rightarrow} 0 \overset{7}{\rightarrow} 1$; (3) $2 \overset{7}{\rightarrow} 3 \overset{7}{\rightarrow} 4 \overset{1}{\rightarrow} 2 \overset{7}{\rightarrow} 3$; (4) $3 \overset{7}{\rightarrow} 4 \overset{1}{\rightarrow} 2 \overset{7}{\rightarrow} 3 \overset{7}{\rightarrow} 4$; (5) $4 \overset{1}{\rightarrow} 2 \overset{7}{\rightarrow} 3 \overset{7}{\rightarrow} 4 \overset{1}{\rightarrow} 2$. Options (2) and (5) do not maximize the number of diamonds from the first corridor. From options (1), (3), and (4) only option (3) maximizes the number of diamonds from the second corridor so this is the best option for Petar. Note that option (3) does not maximize the number of diamonds from the third corridor, nor does it maximize the total number of diamonds, but it is the only lexicographically greatest sequence. The total number of diamonds Petar will collect is 22, which should be the value returned by the call. ### Constraints - $1 \leq N \leq 2000$ - $1 \leq M \leq 4000$ - $1 \leq K \leq 10^9$ - $0 \leq u[i], v[i] < N$ - $1 \leq d[i] \leq 10^9$ for each $0 \leq i < M$ - It is guaranteed that there is at least one corridor starting from each hall. - **Notice the unusually small memory limit of 4 MB.** ### Subtasks | Subtask | Points | Required subtasks | $N$ | $M$ | $K$ | Additional constraints | | :-: | :-: | :-: | :-: | :-: | :-: | :-: | | 0 | $0$ | - | - | - | - | The examples. | | 1 | $11$ | $0$ | $\leq 10$ | $\leq 20$ | $\leq 10$ | - | | 2 | $10$ | $0-1$ | $\leq 100$ | $\leq 1000$ | $\leq 1000$ | - | | 3 | $26$ | $0-2$ | $\leq 100$ | $\leq 1000$ | $\leq 10^9$ | - | | 4 | $11$ | - | $\leq 2000$ | $=N$ | $\leq 10^9$ | Each hall has exactly one corridor starting from it and exactly one corridor ending in it. | | 5 | $10$ | - | $\leq 2000$ | $\leq 4000$ | $\leq 10^9$ | All $d[i]$ are distinct. | | 6 | $11$ | - | $\leq 2000$ | $\leq 4000$ | $\leq 10^9$ | There is exactly one $d[i] = 2$ ($0 \leq i < M$) and all other values in $d$ are equal to 1. | | 7 | $21$ | $0-6$ | $\leq 2000$ | $\leq 4000$ | $\leq 10^9$ | - |