P1399 [NOI2013] Fast Food Restaurant

Xiao T plans to open a delivery fast food restaurant in city C. The time to deliver to a location is proportional to the length of the shortest path from the restaurant to that location. Xiao T wants to choose a location that minimizes the distance to the farthest customer. Customers are located in $N$ buildings in city C. These $N$ buildings are connected by exactly $N$ bidirectional roads. No two roads connect the same pair of buildings. Between any two buildings, there exists at least one path formed by bidirectional roads. The restaurant can be placed at any building, or at any point on any road (the distances from that point to the two endpoints of the road do not need to be integers). Given the map of city C (the road layout and lengths), find the optimal location for the restaurant and output its distance to the farthest customer.

The first line contains an integer $N$, representing the number of buildings in city C. There are also exactly $N$ bidirectional roads. The next $N$ lines each contain $3$ integers, $A_i,B_i,L_i$ ($1\leq i\leq N$, $L_i>0$), indicating that there is a road between buildings $A_i$ and $B_i$ with length $L_i$.

Output a single real number, rounded and kept to **exactly one decimal place**, representing the distance from the optimal restaurant location to its farthest customer. Note: Your result must have exactly one digit after the decimal point. An incorrect number of decimal places will receive no credit.

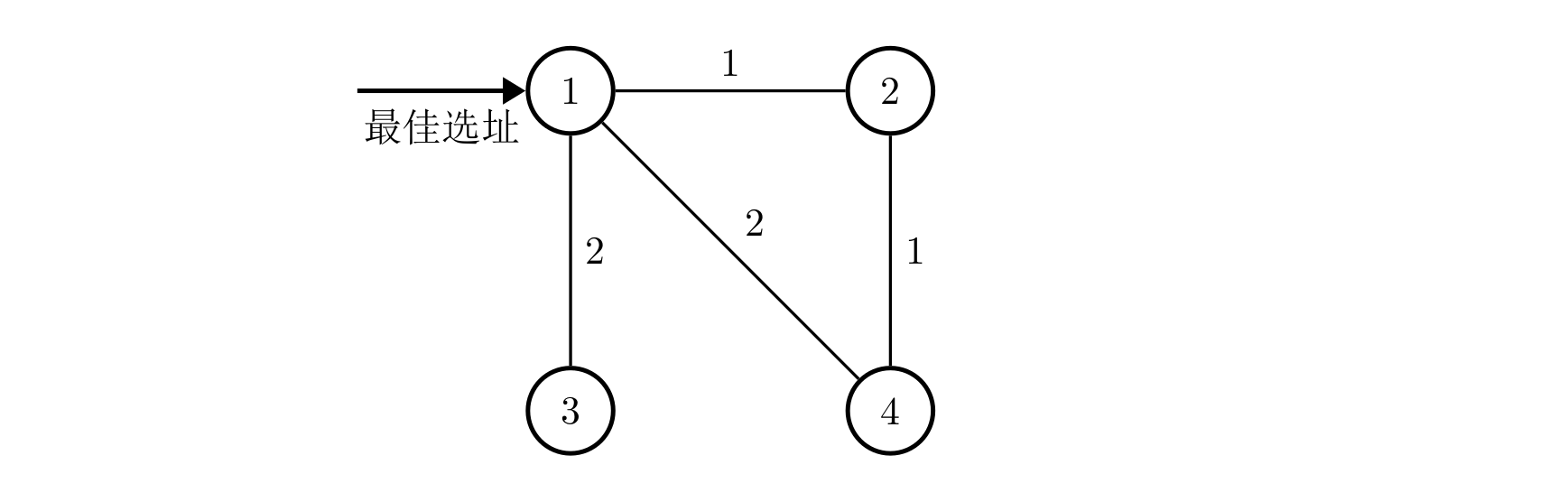
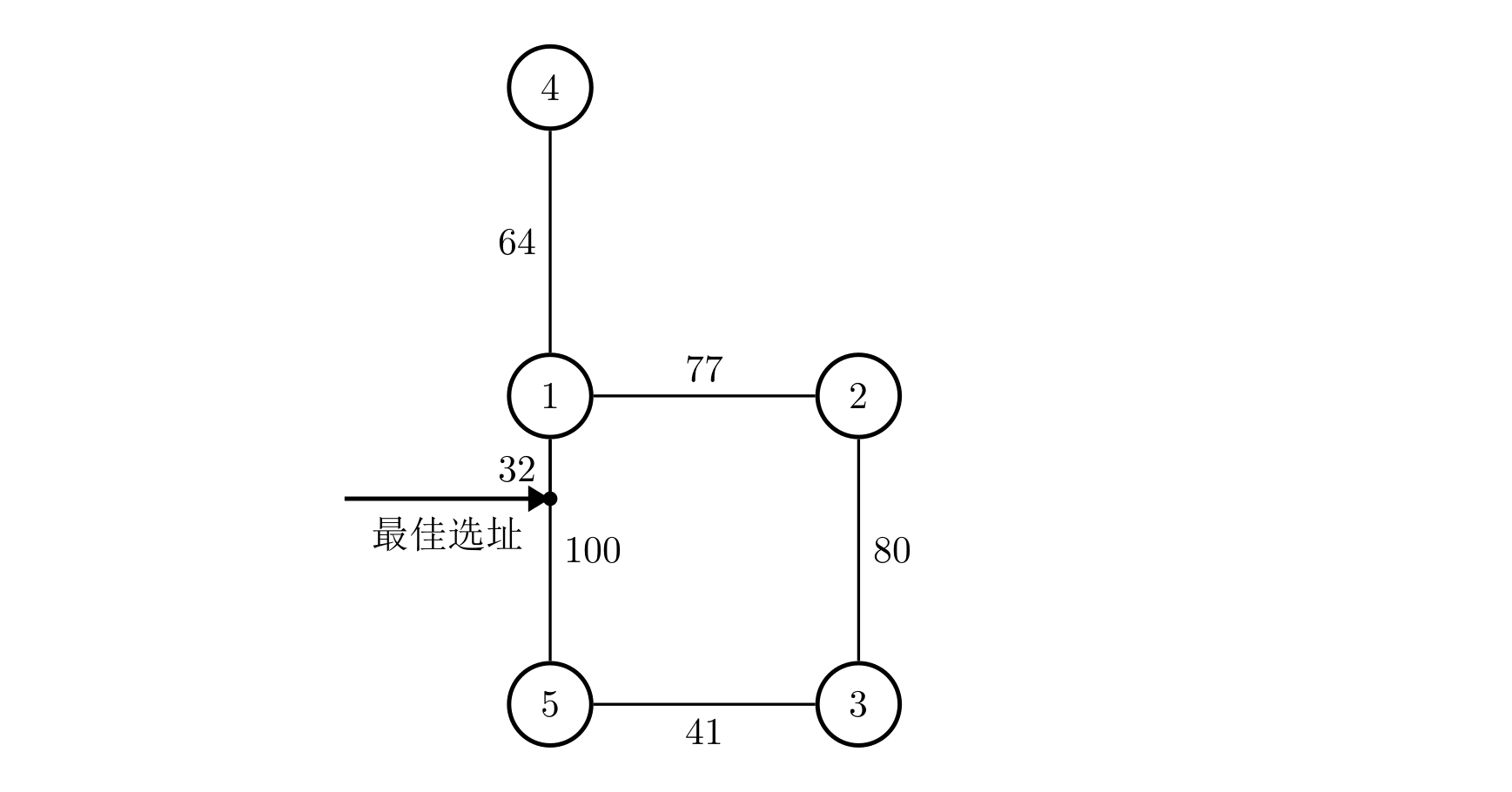
- Sample Explanation 1.  - Sample Explanation 2.  - Constraints: - For $10\%$ of the testdata, $N\leq 80$, $L_i=1$. - For $30\%$ of the testdata, $N\leq 600$, $L_i\leq 100$. - For $60\%$ of the testdata, $N\leq 2000$, $L_i\leq 10^9$. - For $100\%$ of the testdata, $1\leq N\leq 10^5$, $1\leq L_i \leq 10^9$. Translated by ChatGPT 5