P14006 Fate Game

There are $n$ nodes forming a ring. For any positive integer $i \in [1, n]$, there is a bidirectional edge between $i$ and $(i \bmod n) + 1$. There are two pieces, one black and one white. The white piece starts at node $x$, and the black piece starts at node $y$. Each second, both pieces move simultaneously: the white piece moves along one edge in the direction the black piece moved in the previous second (if both pieces were on the same node in the previous second, the white piece does not move), while the black piece can choose to move one edge in either direction or stay in place. You are required to find the number of possible ways in which the two pieces **never occupy the same node at the same time** within $k$ seconds, modulo $998244353$. In this problem, **$n$ is odd**. Two ways are considered different if and only if there exists a moment when the movement direction of at least one piece differs between the two ways.

Four integers $n, x, y, k$.

A single integer representing the answer.

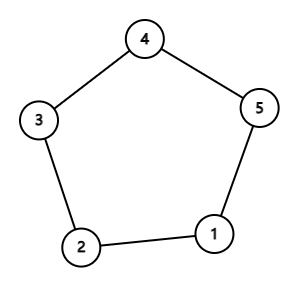
### Sample Explanation For sample 1:  As shown in the figure, the white piece is at node $1$, and the black piece is at node $4$. One possible way is: - In the first second, the white piece moves to node $5$, and the black piece moves to node $3$. - In the second second, the white piece moves to node $4$, and the black piece stays in place. - In the third second, the white piece moves to node $3$, and the black piece moves to node $2$. By enumerating all possibilities, it is easy to find that there are only four valid ways. ### Data Range **This problem uses bundled testing.** | Subtask ID | Special Property | $\tt Subtask$ Score | | :-----------: | :-----------: | :-----------: | | $0$ | $k \leq 3$ | $30$ | | $1$ | $n, k \leq 500$ | $30$ | | $2$ | None | $40$ | For all data, $1 \leq n, k \leq 7 \times 10^3, 1 \leq x, y \leq n$. Translated by ChatGPT 4.1