P14026 [ICPC 2024 Nanjing R] 我将如潮水般归来

那维莱特是枫丹的最高审判官，因其无懈可击的「秉公无私」而闻名。作为世界著名游戏《原神》中的可玩角色，他以其强大的蓄力攻击而闻名，该类攻击可以一次性击中特定范围内的敌人。 由于他非常强大，许多玩家在挑战几乎每个任务时都会使用他。然而，提瓦特中并非所有人都对此感到高兴，尤其是其他 ADC（主要输出角色），比如神里绫华、刻晴等。于是，他们决定说服米哈游在游戏中削弱那维莱特。为此，他们必须提交一份关于那维莱特在一些场景下的伤害报告。 :::align{center}  基于《原神》官方素材制作 ::: 每个战斗场景都发生在一个二维平面上。那维莱特站在 $(0,0)$，最初面朝 $(x_0, y_0)$，进行持续 $t$ 单位时间的蓄力攻击，并以每单位时间 $1$ 弧度的速度逆时针旋转。也就是说，那维莱特会在 $2 \pi$ 单位时间内逆时针转一圈。 考虑从 $(0,0)$ 指向那维莱特面朝方向的射线，攻击范围是距离射线最多为 $d$ 的点的集合。如果目标（一个凸多边形）与攻击范围有公共点，它将每单位时间受到 $1$ 点持续伤害。 作为一名经验丰富的程序员，您被绫华召唤。这次，您的任务是计算目标在前 $t$ 单位时间内所遭受的伤害。

每个测试文件仅有一组测试数据。 第一行输入五个整数 $n$，$x_0$，$y_0$，$d$ 和 $t$（$3 \le n \le 100$，$-10^4 \le x_0, y_0 \le 10^4$，$x_0^2 + y_0^2 > 0$，$1 \le d, t \le 10^4$）。 对于接下来 $n$ 行，第 $i$ 行输入两个整数 $x_i$ 和 $y_i$（$-10^4 \le x_i, y_i \le 10^4$），表示凸多边形第 $i$ 个顶点的坐标。 所有 $n$ 个顶点按逆时针顺序给出，并且任意三个顶点不共线。另外保证该形状与以 $(0,0)$ 为中心、半径为 $d$ 的圆没有公共点。也就是说，不存在一个点既在凸多边形的内部或边界上，同时又在圆的内部或边界上。

输出一行一个实数，表示目标在前 $t$ 单位时间内所遭受的伤害。 如果您的答案的绝对误差或相对误差不超过 $10^{-6}$，则将被视为正确。更正式地，假设您的输出为 $a$，标准答案为 $b$，当且仅当 $\frac{|a - b|}{\max(1, |b|)} \le 10^{-6}$ 时，您的输出才会被接受。

下图同时展示了各个样例数据的初始状态。 :::align{center}  :::
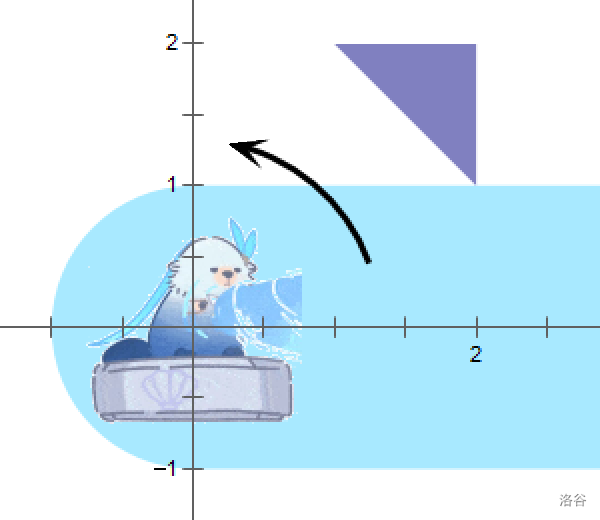