P14051 [SDCPC 2019] Triangle City

三角城是一座拥有 $\frac{n(n+1)}{2}$ 个交叉路口的城市，这些交叉路口被排列成 $n$ 行 $n$ 列，其中第 $i$ 行有 $i$ 个交叉路口。 这些交叉路口通过双向道路相连。形式化地，令 $(i, j)$ 表示第 $i$ 行第 $j$ 列的交叉路口，对于所有 $1 \le j \le i < n$： - 存在一条长度为 $a_{i, j}$ 的道路连接交叉路口 $(i, j)$ 和 $(i + 1, j)$； - 存在一条长度为 $b_{i, j}$ 的道路连接交叉路口 $(i, j)$ 和 $(i + 1, j + 1)$； - 存在一条长度为 $c_{i, j}$ 的道路连接交叉路口 $(i + 1, j)$ 和 $(i + 1, j + 1)$。 此外，对于所有 $1 \le j \le i < n$，都存在一组三边分别为 $a_{i, j}$、$b_{i, j}$ 和 $c_{i, j}$ 的三角形，这正是这座城市被称为“三角城”的原因！ 著名旅行家 BaoBao 刚刚抵达三角城，他计划从交叉路口 $(1, 1)$ 出发，在交叉路口 $(n, n)$ 结束旅程。为了充分享受美景，BaoBao 希望找到一条从 $(1, 1)$ 到 $(n, n)$ 的最长路径，要求每条道路最多经过一次。请帮助 BaoBao 寻找这样一条最长的路径。 请注意，如果一个三角形的三条边长分别为 $a$，$b$，$c$，那么一定有 $a + b > c$，$a + c > b$ 且 $b + c > a$。

有多组测试数据。输入的第一行为一个整数 $T$，表示测试数据组数。对于每组测试数据： 第一行为一个整数 $n$（$2 \le n \le 300$），表示城市的规模。 接下来的 $n-1$ 行，第 $i$ 行包含 $i$ 个整数 $a_{i, 1}, a_{i, 2}, \dots, a_{i, i}$（$1 \le a_{i, j} \le 10^9$），表示连接交叉路口 $(i, j)$ 和 $(i+1, j)$ 的道路长度。 再接下来的 $n-1$ 行，第 $i$ 行包含 $i$ 个整数 $b_{i, 1}, b_{i, 2}, \dots, b_{i, i}$（$1 \le b_{i, j} \le 10^9$），表示连接交叉路口 $(i, j)$ 和 $(i+1, j+1)$ 的道路长度。 再接下来的 $n-1$ 行，第 $i$ 行包含 $i$ 个整数 $c_{i, 1}, c_{i, 2}, \dots, c_{i, i}$（$1 \le c_{i, j} \le 10^9$），表示连接交叉路口 $(i+1, j)$ 和 $(i+1, j+1)$ 的道路长度。 保证所有测试数据中 $n$ 的总和不超过 $5 \times 10^3$。

对于每组测试数据，输出三行。 第一行输出一个整数 $l$，表示从 $(1, 1)$ 到 $(n, n)$ 的最长路径长度，且每条道路最多经过一次。 第二行输出一个整数 $m$，表示最长路径上经过的交叉路口数量。 第三行输出 $2m$ 个用空格隔开的整数 $i_1, j_1, i_2, j_2, \dots, i_m, j_m$，其中 $(i_k, j_k)$ 表示最长路径上的第 $k$ 个交叉路口。根据题意，保证有 $(i_1, j_1) = (1, 1)$ 且 $(i_m, j_m) = (n, n)$。 如果有多组合法解答，可以输出任意一组。 请勿在每一行行末输出多余的空格，否则你的解答可能会被判错！

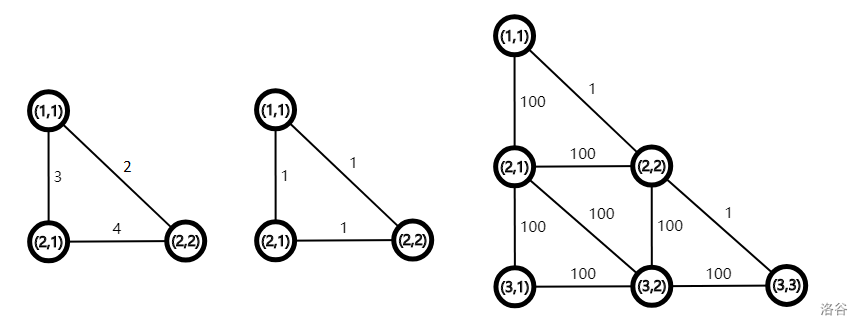
样例测试数据如下所示： :::align{center}  ::: 由 ChatGPT 5 翻译