P14096 [ICPC 2023 Seoul R] Walk Swapping

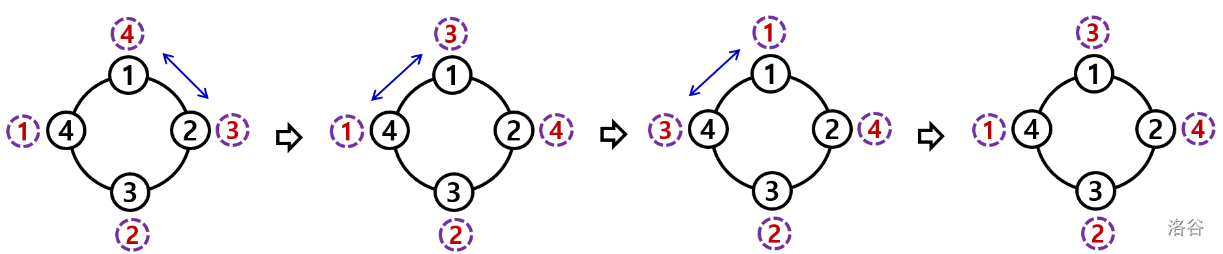
一个有 $n$ 个顶点的环 $C$ 是一个图，其中第 $i$ 个顶点和第 $i+1$ 个顶点（对于 $i=1,2,\dots,n-1$）通过一条边相连，并且第 $n$ 个顶点和第 $1$ 个顶点也通过一条边相连，其中 $C$ 的顶点编号为 $1$ 到 $n$。 有 $n$ 个硬币，每个硬币编号为 $1$ 到 $n$ 中的一个数，且不同硬币的编号可以相同。最初，$C$ 的每个顶点上都放有一个硬币。然后，任意两个顶点可以互相交换各自的硬币。对于环 $C$ 上的一条路径 $w=(v_1, v_2, \dots, v_k)$，可以依次按 $i=1,2,\dots,k-1$ 的顺序，将 $v_i$ 和 $v_{i+1}$ 上的硬币交换，称为一次路径交换。这里，路径 $w$ 是由 $k$（$k \geq 1$）个顶点依次组成的序列，相邻两个顶点不同且在 $C$ 中相邻，可以理解为遍历 $C$ 时依次经过的顶点。$k$ 称为路径 $w$ 的长度。对于长度 $k \geq 2$ 的路径，路径交换过程中会发生 $k-1$ 次硬币交换；对于长度为 1 的路径，则没有交换。如图所示，是在一个有 4 个顶点的环上按照路径 $(2, 1, 4, 1)$ 进行路径交换的过程：  现在给定 $C$ 的初始硬币分布以及目标硬币分布，你需要通过若干次路径交换，使得初始分布变为目标分布，并且使交换的总次数最小。 例如，在上图中，路径交换 $(2, 1, 4, 1)$ 共交换了 3 次，但通过路径 $(1, 2)$ 一次交换也可以得到相同的目标配置。 给定环 $C$ 的顶点数量、初始硬币分布和目标硬币分布，编写程序输出将初始配置变为目标配置所需路径交换中最少的硬币交换次数。 如果不存在任何一种路径交换能够得到目标配置，输出 -1。

输入从标准输入读入。 第一行包含一个整数 $n$，表示环 $C$ 的顶点数，$1 \leq n \leq 3000$。 第二行包含 $n$ 个整数，第 $i$ 个整数表示初始时第 $i$ 个顶点上的硬币编号（可能有重复），所有值均为 $1$ 到 $n$ 之间的整数。 第三行包含 $n$ 个整数，第 $i$ 个整数表示目标状态下第 $i$ 个顶点上的硬币编号（可能有重复），所有值均为 $1$ 到 $n$ 之间的整数。

输出一个整数，表示通过路径交换变换为目标配置时，最少硬币交换次数。如果无法达到目标配置，输出 -1。

由 ChatGPT 5 翻译