P14108 [ZJCPC 2017] Domino Tiling

Chiaki has an $n \times m$ rectangular chessboard. She would like to tile this board with dominoes, where a domino is a $2 \times 1$ rectangle, such that: - all the squares of the board are covered but no dominoes overlap or lie partially off the board. - there must be no points where corners of four different dominoes meet. 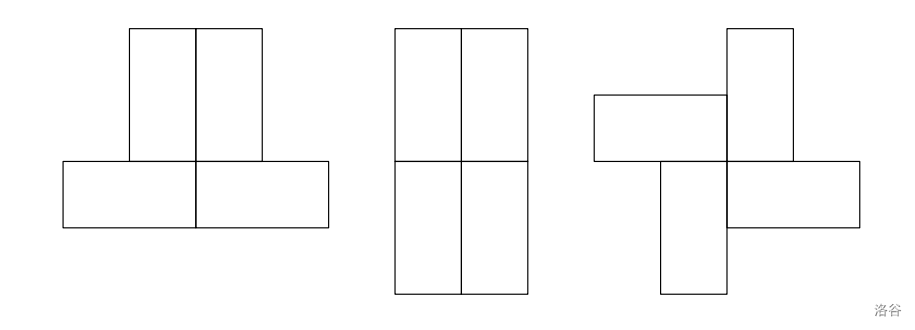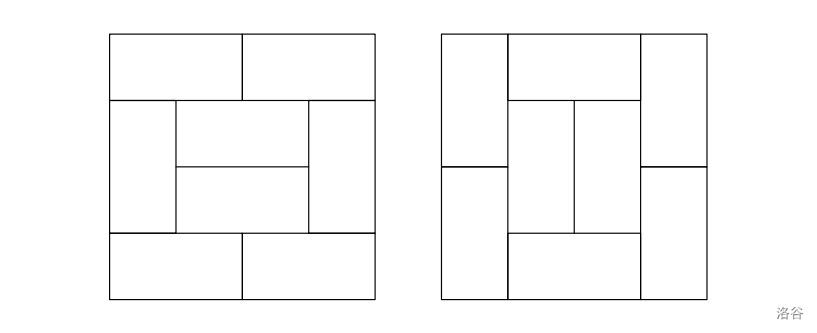The figure below shows some forbidden configurations: :::align{center}  ::: The figure below shows two valid tilings of $4 \times 4$ chessboard: :::align{center}  ::: You also need to number the dominoes of chessboard so that no two dominoes have the same number. You can use the number from $1$ to $n \times m$.

There are multiple test cases. The first line of input contains an integer $T$, indicating the number of test cases. For each test case: The first line contains two integers $n$ and $m$ $(1 \le n, m \le 100)$ -- the size of the rectangular chessboard. It is guaranteed that the sum of $n \times m$ over all test cases does not exceed $2 \times 10^6$.

For each test case, output a valid chessboard described above. A valid chessboard consists of $n$ lines and each line contains $m$ integers. Each integer in the output should represent the $id$ of a domino. The grids sharing the same $id$ belong to the same domino. If there is no solution, output "Impossible!"" (without the quotes) instead.