P14110 [ZJCPC 2017] Final Defense Line

在平面上有一个圆，这个圆的圆心坐标和半径都是未知的。 Chiaki 发现了平面上的三个不同的点 $A$、$B$ 和 $C$。她知道每个点到这个圆的圆周的最短距离。 Chiaki 希望根据上述信息求出满足条件的最小的圆。 注意，一般来说，半径为无穷大的圆就是一条直线。但在本题中，直线不被认为是圆。

有多组测试数据。输入的第一行为一个整数 $T$（$1 \le T \le 2 \times 10^5$），表示测试数据的组数。对于每组测试数据： 第一行包含三个整数 $x_a$、$y_a$ 和 $d_a$（$-100 \le x_a \le 100, y_a = 0, 1 \le d_a \le 100$），表示点 $A$ 的坐标及其到圆周的最短距离。 第二行包含三个整数 $x_b$、$y_b$ 和 $d_b$（$-100 \le x_b \le 100, y_b = 0, 1 \le d_b \le 100$），表示点 $B$ 的坐标及其到圆周的最短距离。 第三行包含三个整数 $x_c$、$y_c$ 和 $d_c$（$-100 \le x_c, y_c, d_c \le 100, d_c \ne 0$），表示点 $C$ 的坐标及其到圆周的最短距离。 当距离等于 $0$ 时，点在圆周上。当距离大于 $0$ 时，点在圆内。当距离小于 $0$ 时，点在圆外，且最短距离的绝对值就是距离。 保证最小可能的圆半径不超过 $10^4$。

对于每组测试数据，如果存在无穷多个圆，输出一行 $-1$。如果无解，输出一行 $0$。否则，输出一个整数 $m$ 和一个实数 $r$，中间用空格分隔，表示满足条件的圆的个数以及最小圆半径 $r$。如果你的答案相对误差不超过 $10^{-6}$，即可被接受。

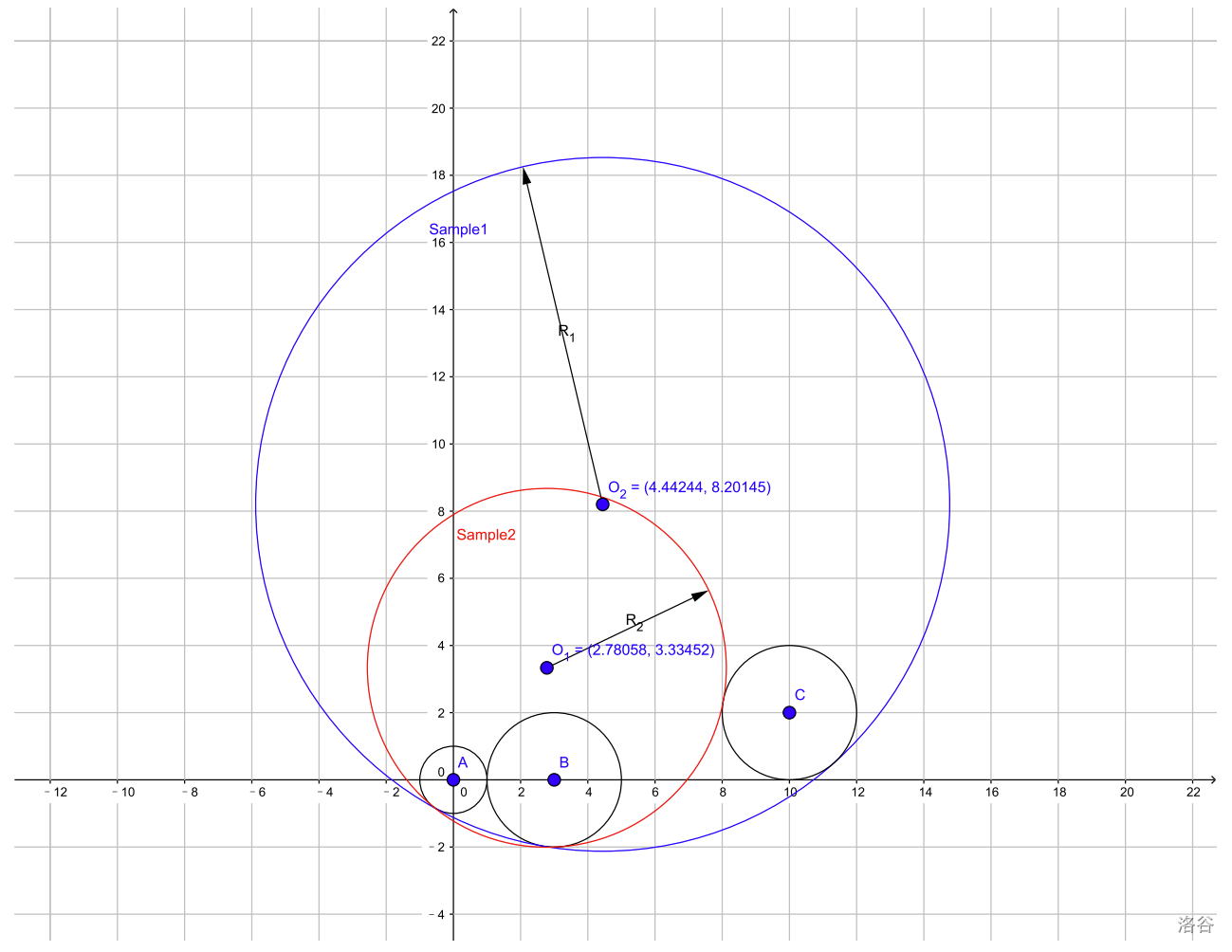
下图展示了样例情况。 :::align{center}  ::: 由 ChatGPT 5 翻译