P14122 [SCCPC 2021] Direction Setting

给定一个包含 $n$ 个顶点和 $m$ 条边的无向图，第 $i$ 个顶点有一个限制 $a_i$。请为每条边分配一个方向，使得整个图变为有向图，并且使下述值 $D$ 最小： $$ D = \sum\limits_{i=1}^n \max(0, d_i - a_i) $$ 其中 $d_i$ 表示第 $i$ 个顶点的入度（即指向该顶点的边的条数）。

存在多组测试数据。输入的第一行为一个整数 $T$，表示测试数据组数。对于每组测试数据： 第一行包含两个整数 $n$ 和 $m$（$2 \le n \le 300$，$1 \le m \le 300$），表示顶点数和边数。 第二行包含 $n$ 个整数 $a_1, a_2, \cdots, a_n$（$0 \le a_i \le 10^4$），其中 $a_i$ 表示第 $i$ 个顶点的限制。 接下来的 $m$ 行，每行包含两个整数 $u_i$ 和 $v_i$（$1 \le u_i, v_i \le n$），表示有一条边连接顶点 $u_i$ 和 $v_i$。注意可能存在自环或重边。 保证所有测试数据中 $n$ 与 $m$ 的总和不超过 $3\times10^3$。

对于每组测试数据输出两行。第一行输出一个整数，表示最小的 $D$。第二行输出一个长度为 $m$ 的字符串 $s_1s_2\cdots s_m$，仅包含字符 `0` 和 `1`，表示每条边的定向分配方案以达到最小的 $D$。如果 $s_i = \text{`0'}`，则第 $i$ 条边从 $u_i$ 指向 $v_i$；否则从 $v_i$ 指向 $u_i$。如果存在多组合法方案，可以输出任意一种。

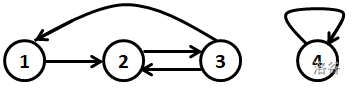
第一个样例测试数据如图所示： :::align{center}  ::: 由 ChatGPT 5 翻译