P14122 [SCCPC 2021] Direction Setting

Given an undirected graph with $n$ vertices and $m$ edges where the $i$-th vertex has a limit $a_i$, please assign a direction for each edge so that the graph becomes directed and the following value $D$ is minimized. $$D = \sum\limits_{i=1}^n \max(0, d_i - a_i)$$ where $d_i$ is the in-degree (that is, the number of edges going into that vertex) of the $i$-th vertex.

There are multiple test cases. The first line of the input contains an integer $T$ indicating the number of test cases. For each test case: The first line contains two integers $n$ and $m$ ($2 \le n \le 300$, $1 \le m \le 300$) indicating the number of vertices and edges. The second line contains $n$ integers $a_1, a_2, \cdots, a_n$ ($0 \le a_i \le 10^4$) where $a_i$ indicates the limit of the $i$-th vertex. For the following $m$ lines, the $i$-th line contains two integers $u_i$ and $v_i$ ($1 \le u_i, v_i \le n$) indicating that there is an edge connecting vertex $u_i$ and $v_i$. Note that there might be self loops or multiple edges. It's guaranteed that neither the sum of $n$ nor the sum of $m$ of all test cases will exceed $3 \times 10^3$.

For each test case output two lines. The first line contains an integer indicating the smallest possible $D$. The second line contains a string $s_1s_2\cdots s_m$ of length $m$ consisting only of `0`s and `1`s indicating a direction assignment plan of the edges to achieve the smallest possible $D$. If $s_i = \text{`0'}$ then the $i$-th edge is going from $u_i$ into $v_i$; Otherwise it's going from $v_i$ into $u_i$. If there are multiple valid answers you can output any of them.

The first sample test case is shown as follows. :::align{center}  :::
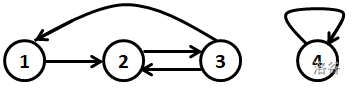