P14157 [ICPC 2022 Nanjing R] 树的染色

有一棵 $n$ 个节点的有根树。节点编号从 $1$ 到 $n$（含两端），其中节点 $1$ 是根节点。一开始所有 $n$ 个节点都是白色的，您需要将所有节点染成黑色。 为了帮助您达成目标，我们提供 $n$ 种操作，编号从 $0$ 到 $(n - 1)$（含两端）。操作 $i$（$0 \le i \le n - 1$）需要您首先选择一个节点 $u$，之后将所有满足以下条件的节点 $v$ 染成黑色： - 节点 $v$ 在以 $u$ 为根的子树里，也就是说 $u = v$ 或 $u$ 是 $v$ 的祖先节点。 - 节点 $u$ 与 $v$ 之间的距离恰为 $i$。节点 $u$ 与 $v$ 之间的距离指的是从 $u$ 走到 $v$ 需要经过的最少边数。 执行一次操作 $i$ 的代价是 $a_i$。一个节点可以被多次染色，所有操作都可以被执行任意次。求将所有节点染成黑色的最小总代价。

有多组测试数据。第一行输入一个整数 $T$ 表示数据组数，对于每组测试数据： 第一行输入一个整数 $n$（$2 \le n \le 10^5$）表示树的大小。 第二行输入 $n$ 个整数 $a_0, a_1, \cdots, a_{n-1}$（$1 \le a_i \le 10^9$），其中 $a_i$ 表示执行一次操作 $i$ 的代价。 对于接下来 $(n - 1)$ 行，第 $i$ 行输入两个整数 $u_i$ 和 $v_i$（$1 \le u_i, v_i \le n$，$u_i \neq v_i$）表示有一条边连接节点 $u_i$ 和 $v_i$。 保证所有数据 $n$ 之和不超过 $3 \times 10^5$。

每组数据输出一行一个整数，表示染黑整棵树的最小总代价。

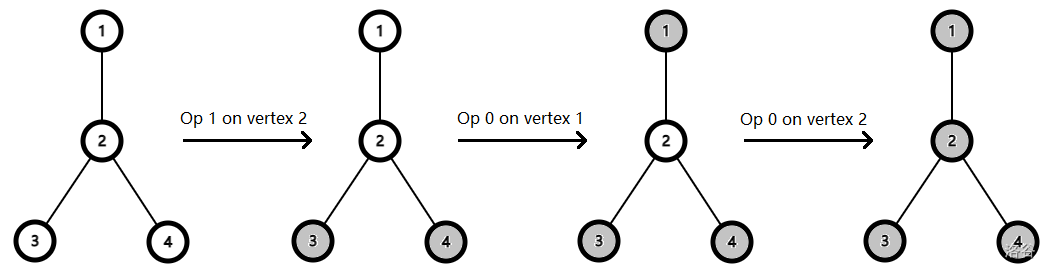
第一组样例数据如下所示。答案是 $15 + 10 + 10 = 35$。 :::align{center}  ::: 第二组样例数据如下所示。答案是 $5 + 10 + 1 + 1 = 17$。 :::align{center}  :::
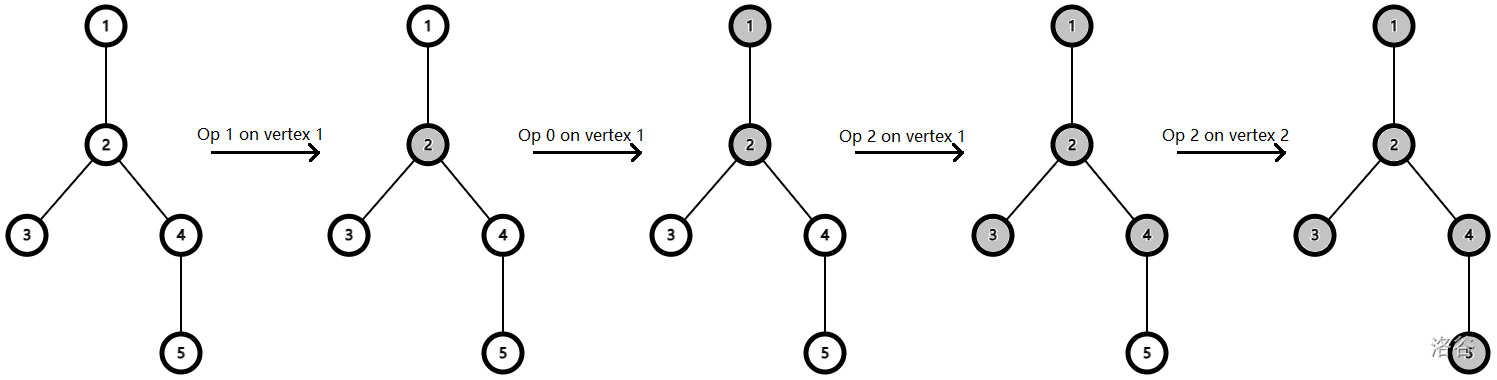