P14158 [ICPC 2022 Nanjing R] 三角形
题目描述
平面上有一个正方形。正方形左下角、左上角、右下角和右上角的坐标分别是 $(0,0)$,$(0,10^9)$,$(10^9,0)$ 和 $(10^9,10^9)$。
给定一个正整数 $k$,您需要将该正方形分割成恰好 $k$ 个锐角三角形。也就是说,找到 $k$ 个锐角三角形满足任意两个三角形不相交(但它们可以有一个公共点或一条公共线段)且所有三角形的并等于该正方形。
输入格式
每个测试文件仅有一组测试数据。
第一行输入一个整数 $k$($1 \leq k \leq 50$)。
输出格式
如果不存在合法分割,输出 "No"(不输出引号)。
否则首先输出一行 "Yes"(不输出引号)。接下来 $k$ 行每行输出六个由单个空格分割的数 $x_1$,$y_1$,$x_2$,$y_2$,$x_3$ 和 $y_3$ 表示 $(x_1, y_1)$,$(x_2, y_2)$ 和 $(x_3, y_3)$ 这三个点构成一个锐角三角形。请注意,这 $k$ 个锐角三角形必须是正方形的一个分割。
为了避免精度问题,我们额外限制所有三角形顶点的坐标都必须是整数。可以证明,对于本题所有可能的输入,如果正方形可以被分割成 $k$ 个锐角三角形,则一定存在一个满足所有限制的分割。
说明/提示
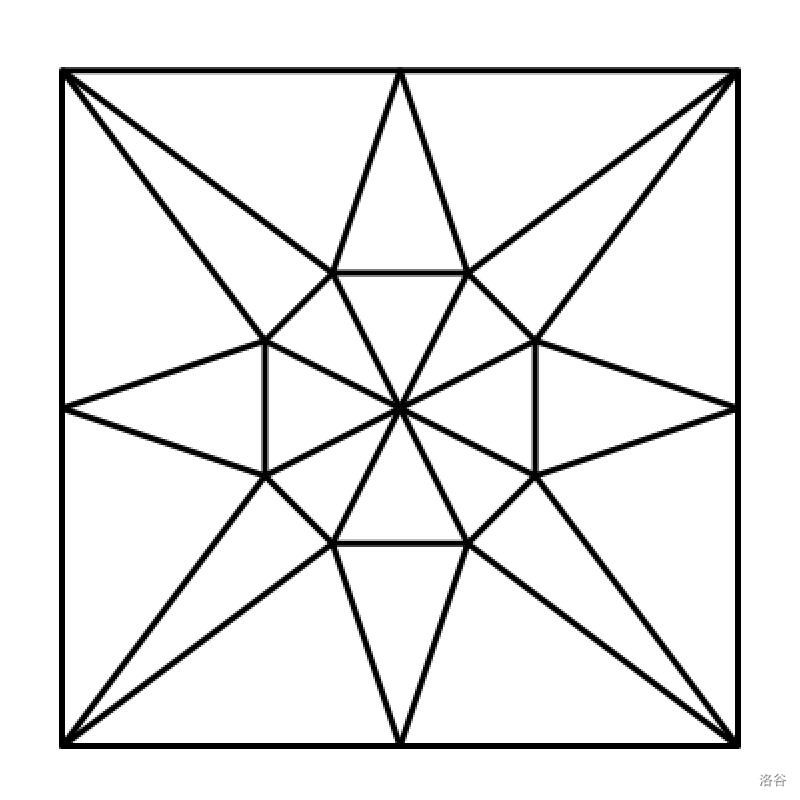
下图展示了第二组样例数据中的分割方案。
:::align{center}
:::