P14160 [ICPC 2022 Nanjing R] 工厂重现
题目描述
有一片由 $n$ 座城市组成的王国。城市的编号从 $1$ 到 $n$(含两端)且有 $(n - 1)$ 条道路连接各个城市。对于任意两座城市,居民们都可以沿着这些道路互相访问。
皇后最近决定建设 $k$ 座新的工厂。为了防止污染,她规定每座城市最多只能建立一座工厂。
您作为皇家设计师,需要在规划建设的同时,求出两两工厂之间距离之和的最大值。
两座工厂之间的距离,即为两座工厂所在的两座城市之间的最短路径长度。路径的长度即为路径中所有边的长度之和。
输入格式
每个测试文件仅有一组测试数据。
第一行输入两个整数 $n$ 和 $k$($2\le n \le 10^5$,$2 \le k \le n$)表示城市的数量与新建工厂的数量。
对于接下来 $(n - 1)$ 行,第 $i$ 行输入三个整数 $u_i$,$v_i$ 和 $w_i$($1 \le u_i, v_i \le n$,$u \neq v$,$1 \le w \le 10^4$)表示有一条道路连接城市 $u_i$ 与 $v_i$,其长度为 $w_i$。
输出格式
输出一行一个整数表示两两工厂之间距离之和的最大值。
说明/提示
样例数据解释如下。
:::align{center}
:::
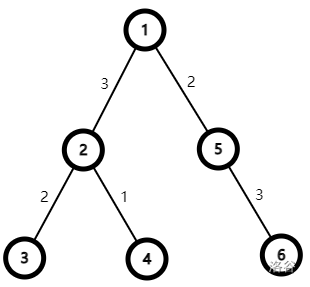
可以选择在城市 $3$,$4$ 和 $6$ 建立工厂。令 $d(i, j)$ 表示城市 $i$ 与 $j$ 之间的最短路径长度,则答案为 $d(3, 4) + d(3, 6) + d(4, 6) = 3 + 10 + 9 = 22$。