P14165 [ICPC 2022 Nanjing R] 清空水箱
题目描述
自来水厂最近建造了一种多边形水箱,水箱的厚度可以忽略不计。
为了启用水箱,工程师们准备在水箱上安装若干出水阀门。一个出水阀门可以被看作水箱上的一个点,当阀门打开时,水箱里的水会从阀门流出。
:::align{center}
:::
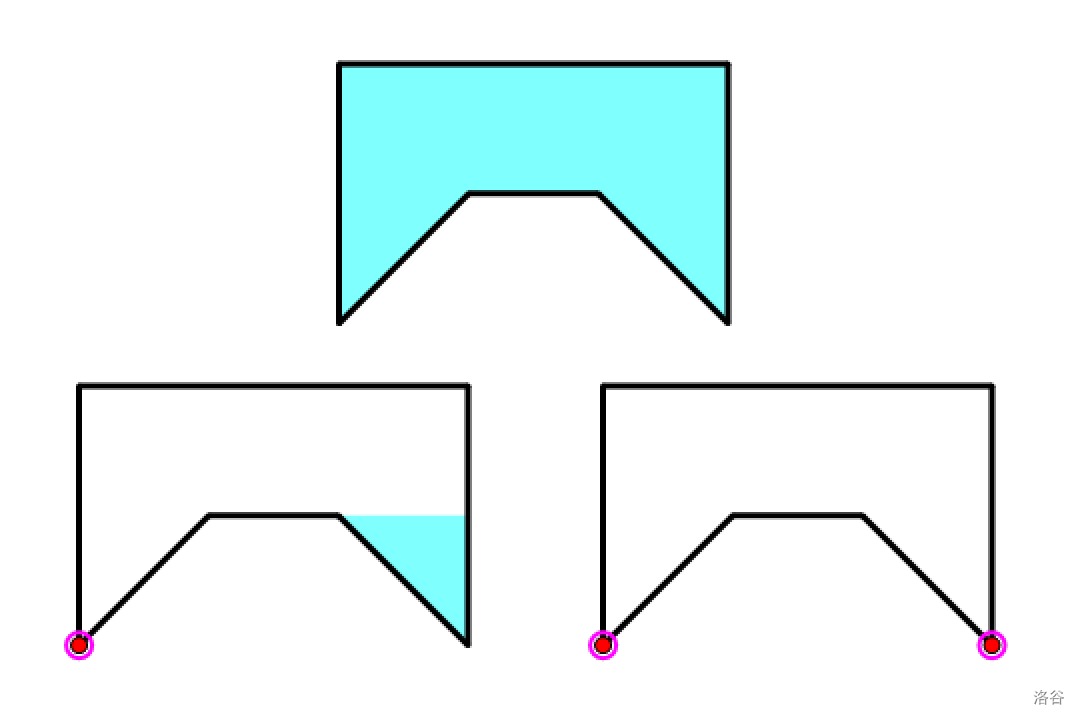
如上图所示,紫色的点代表阀门,而浅蓝色区域代表阀门全部打开后水箱内剩余的水。
作为总工程师的您需要知道,至少需要安装多少个出水阀门,才能在所有阀门同时打开后,让水箱里的水全部流出。
您可以认为水是一种理想流体且环境中不存在大气压,因此水总有流向更低处的趋势,即使位于水平平面上也是如此。
输入格式
每个测试文件仅有一组测试数据。
第一行输入一个整数 $n$($3 \le n \le 2 \times 10^3$)表示多边形(也就是水箱的形状)的顶点数。
对于接下来 $n$ 行,第 $i$ 行输入两个整数 $x_i$ 和 $y_i$($|x_i|, |y_i| \le 10^4$)表示多边形第 $i$ 个顶点的坐标。顶点按逆时针顺序给出。
给定的多边形是简单多边形。也就是说,多边形的顶点两两不同,且除了相邻边存在公共顶点外,不存在两条边有公共点。$\textbf{\LARGE{不}}$保证相邻边不共线。
输出格式
输出一行一个整数表示清空水箱至少需要多少个出水阀门。
说明/提示
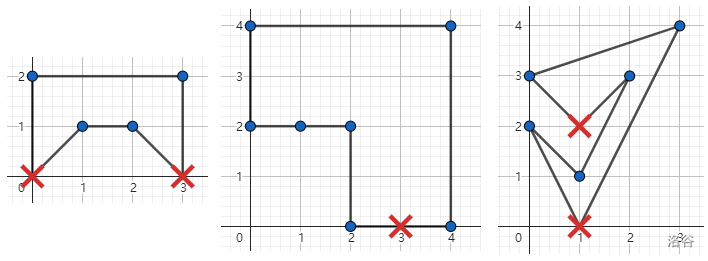
对于第一组样例数据,在 $(0,0)$ 与 $(3,0)$ 安装两个出水阀门即可清空水箱。
对于第二组样例数据,在 $(3,0)$ 安装一个出水阀门即可清空水箱。事实上,只要把该出水阀门安装在满足 $2 \le x \le 4$ 的 $(x, 0)$ 即可。
对于第三组样例数据,在 $(1,0)$ 与 $(1,2)$ 安装两个出水阀门即可清空水箱。
:::align{center}
:::