P14244 [CCPC 2024 Shandong I] 阻止城堡

一块有 $10^9$ 行和 $10^9$ 列的棋盘上放着 $n$ 个城堡与 $m$ 个障碍物。每个城堡或障碍物恰好占据一个格子，且被占据的格子两两不同。两座城堡可以互相攻击，若它们位于同一行或同一列，且它们之间没有障碍物或其它城堡。更正式地，令 $(i, j)$ 表示位于第 $i$ 行第 $j$ 列的格子，位于 $(i_1, j_1)$ 和 $(i_2, j_2)$ 的两座城堡可以互相攻击，若以下条件中有一条成立： - $i_1 = i_2$，且对于所有 $\min(j_1, j_2) < j < \max(j_1, j_2)$，不存在位于 $(i_1, j)$ 的障碍物或城堡。 - $j_1 = j_2$，且对于所有 $\min(i_1, i_2) < i < \max(i_1, i_2)$，不存在位于 $(i, j_1)$ 的障碍物或城堡。 找出一种方法，向棋盘上额外添加最少的障碍物，使得任意两座城堡都不能互相攻击。请注意：不能将额外的障碍物放在已经被占据的格子里。

有多组测试数据。第一行输入一个整数 $T$ 表示测试数据组数，对于每组测试数据： 第一行输入一个整数 $n$（$2 \le n \le 200$）表示城堡的数量。 对于接下来 $n$ 行，第 $i$ 行输入两个整数 $r_i$ 和 $c_i$（$1 \le r_i, c_i \le 10^9$），表示第 $i$ 座城堡位于第 $r_i$ 行第 $c_i$ 列。 接下来的一行输入一个整数 $m$（$0 \le m \le 200$）表示障碍物的数量。 对于接下来 $m$ 行，第 $i$ 行输入两个整数 $r'_i$ 和 $c'_i$（$1 \le r'_i, c'_i \le 10^9$），表示第 $i$ 个障碍物位于第 $r'_i$ 行第 $c'_i$ 列。 保证被占据的格子两两不同。同时保证所有数据 $n$ 之和与 $m$ 之和均不超过 $400$。

对于每组数据： 如果能阻止城堡之间互相攻击，首先输出一行一个整数 $k$，表示最少需要额外添加多少障碍物。接下来输出 $k$ 行，其中第 $i$ 行包含两个由单个空格分隔的整数 $x_i$ 和 $y_i$（$1 \le x_i, y_i \le 10^9$），表示您准备将第 $i$ 个额外障碍物放在格子 $(x_i, y_i)$ 里。如果有多种合法答案，您可以输出任意一种。 如果无法阻止城堡之间互相攻击，只要输出一行 $\texttt{-1}$。

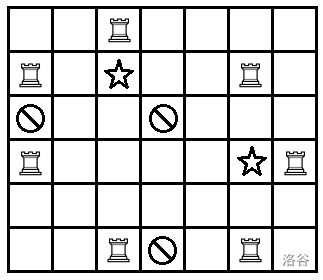
第一组样例数据如下图所示。我们只需要添加 $2$ 个额外的障碍物（图中用星星标识），其中一个位于 $(2, 3)$，另一个位于 $(4, 6)$。 :::align{center}  :::