P14249 [CCPC 2024 Shandong I] 回文多边形
题目描述
给定一个有 $n$ 个顶点的凸多边形。顶点按逆时针顺序编号从 $1$ 到 $n$(含两端),第 $i$ 个顶点有一个权值 $f(i)$。
称一个顶点的子集是回文的,若它们的权值能够按逆时针顺序组成一个回文序列。更正式地,设子集里有 $k$ 个顶点,它们的编号按逆时针顺序为 $v_0, v_1, \cdots, v_{k - 1}$。需要存在一个整数 $d$ 满足 $0 \le d < k$,且对于所有 $0 \le i < k$ 有 $f(v_{(d + i) \bmod k}) = f(v_{(d - 1 - i) \bmod k})$。
在所有回文的顶点子集中,找出凸包面积最大的子集。
输入格式
有多组测试数据。第一行输入一个整数 $T$ 表示测试数据组数。对于每组测试数据:
第一行输入一个整数 $n$($3 \le n \le 500$)表示凸多边形的顶点数。
第二行输入 $n$ 个整数 $f(1), f(2), \cdots, f(n)$($1 \le f(i) \le 10^9$),其中 $f(i)$ 表示第 $i$ 个顶点的权值。
对于接下来的 $n$ 行,第 $i$ 行输入两个整数 $x_i$ 和 $y_i$($-10^9 \le x_i, y_i \le 10^9$)表示第 $i$ 个顶点的坐标。顶点按逆时针顺序列出。保证凸多边形的面积为正,且没有重合的顶点。但可能存在三点共线的情况。
保证所有数据 $n$ 之和不超过 $10^3$。
输出格式
每组数据输出一行一个整数,表示回文顶点子集的最大凸包面积乘以 $2$。可以证明这个值总是一个整数。
说明/提示
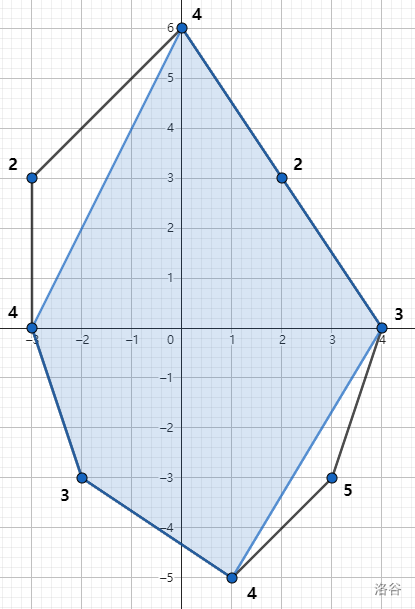
第一组样例数据如下图所示。选择顶点 $2$,$4$,$5$,$6$,$8$,并考虑 $d = 1$,权值序列 $\{4, 3, 4, 3, 4\}$ 是一个回文序列。
:::align{center}
:::