P14254 分割（divide）

你是洛咕咕王国的土地测绘官。洛咕咕王国并购了一块新的领土，这块新的领土正等待被分配。 这块领土可被认为是一棵有 $n$ 个结点、结点编号为 $1$ 到 $n$ 的树，根为编号 $1$。为了便于表述，我们把每个结点 $i$ 在原树中的深度记作 $d_i$，并规定根的深度为 $1$。 你的王国有若干位诸侯希望购买土地，因此现在要从这棵树中选出 $k$ 个**两两不同**的结点，并把它们的编号排成一个有序序列 $b=(b_1,b_2,\dots,b_k)$。这个序列必须满足两个条件： 第一，每个被选的结点都不是根，并且它们的深度是非降的，也就是对所有 $1\le i

第一行包含两个正整数 $n,k$，分别表示树的结点个数和需要选出的结点个数。 第二行包含 $n-1$ 个正整数，第 $i$ 个正整数表示结点 $(i+1)$ 的父结点的编号 $p_i$。根结点 $1$ 没有父结点。

输出一行一个整数，表示满足题目条件的序列 $b$ 的个数，结果对 $998244353$ 取模。

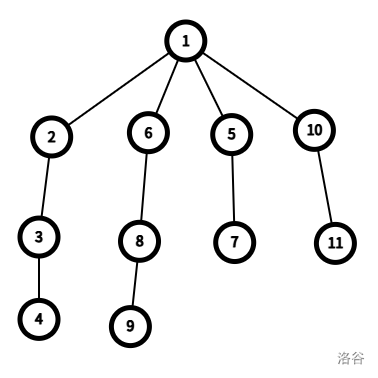
**【样例解释 #1】** 如图，合法的序列 $b$ 一共有 $4$ 个，分别是： - 令 $b_1 = 5, b_2 = 10$； - 令 $b_1 = 10, b_2 = 5$； - 令 $b_1 = 7, b_2 = 11$； - 令 $b_1 = 11, b_2 = 7$。 :::align{center}  ::: 以 $b_1 = 5, b_2 = 10$ 为例，$d_5 = 2$ 且 $d_{10} = 2$，有 $d_5 \le d_{10}$。当我们切断结点 $5$ 和 $10$ 与其父结点 $1$ 的连边后，原树被分割成三棵子树。第一棵子树以 $b_1=5$ 为根，包含结点 $\{5, 7\}$；第二棵子树以 $b_2=10$ 为根，包含结点 $\{10, 11\}$；第三棵子树则是包含原树根 $1$ 的剩余部分。 对于第一棵子树，其结点在**原树**中的深度为 $\{2, 3\}$，因此 $S_1 = \{2, 3\}$。对于第二棵子树，其结点深度同样为 $\{2, 3\}$，所以 $S_2 = \{2, 3\}$。对于包含根结点的第三棵子树，去重后的深度集合为 $S_3 = \{1, 2, 3, 4\}$。计算交集可得 $S_2 \cap S_3 = \{2, 3\}$，与 $S_1$ 相等。因此 $b_1 = 5, b_2 = 10$ 是一个符合条件的序列。 **【样例解释 #2】** 一个符合条件的序列 $b$ 是 $b_1 = 4, b_2 = 9, b_3 = 12$。 **【样例 #4】** 见选手目录下的 `divide/divide4.in` 与 `divide/divide4.ans`。 这个样例满足测试点 $8$ 的条件限制。 **【样例 #5】** 见选手目录下的 `divide/divide5.in` 与 `divide/divide5.ans`。 这个样例满足测试点 $13$ 的条件限制。 **【样例 #6】** 见选手目录下的 `divide/divide6.in` 与 `divide/divide6.ans`。 这个样例满足测试点 $21\sim 25$ 的条件限制。 ------ **【数据范围】** 本题共 $25$ 个测试点，每个测试点占 $4$ 分，共 $100$ 分。 ::cute-table{tuack} |测试点编号|$n\le$|特殊性质| |:-:|:-:|:-:| |$1\sim 2$|$12$|无| |$3\sim 5$|$10^2$|无| |$6\sim 7$|$2\times 10^3$|无| |$8$|^|A| |$9\sim 10$|$2\times 10^5$|^| |$11\sim 12$|$10^6$|^| |$13$|$2\times 10^5$|B| |$14\sim 15$|$10^6$|^| |$16\sim 20$|$2\times 10^5$|无| |$21\sim 25$|$10^6$|无| 特殊性质 A：$k=2$。 特殊性质 B：树为一棵满 $t$ 叉树，其中 $t \in [3,n)\cap \Z$。 对于 $100\%$ 的数据，保证 $2\le k< n\le10^6$，$1 \leq p_i < i$。树保证连通。