P14260 Counting

Little Y and Little S have a tree with $n$ nodes. Each of them has a game piece. Initially, they arbitrarily choose two points $u_0, v_0$: Little Y places his piece at $u_0$, and Little S places her piece at $v_0$. Subsequently, they move their pieces simultaneously. Each time, they move their own piece along an edge of the tree to an adjacent node. However, if this is not the first move, they cannot move the piece back along the edge used in the previous step. They can move the pieces any number of times. Let the positions of the two pieces after the $i$-th move be $u_i, v_i$, respectively. They call a movement scheme **counted** if for every $i$, the distance between $u_i$ and $v_i$ is equal to the distance between $u_0$ and $v_0$. The distance between two points $u$ and $v$ is defined as the number of edges in the unique simple path between them on the tree. In particular, if the two points are the same, the distance is $0$. Now, they have chosen **two distinct points** $y$ and $s$. They want to know how many different counted movement schemes there are such that Little Y's piece passes through $y$, and Little S's piece passes through $s$. The two pieces **do not need to** pass through these points simultaneously. Formally, there exist $i, j$ such that $u_i = y$ and $v_j = s$, **and it is not required that $i = j$**. Two movement schemes are considered different if and only if the number of moves in the two schemes is different, or for some $i$, at least one of $u_i$ or $v_i$ differs between the two schemes.

**This problem contains multiple test cases.** The first line of input contains a positive integer $T$, representing the number of test cases. This is followed by $T$ test cases, each formatted as follows: The first line contains three integers $n, y, s$, indicating the number of nodes in the tree and the two given points, respectively. **It is guaranteed that $y \neq s$.** The next $n-1$ lines: The $i$-th line contains two integers $a_i, b_i$, indicating that the $i$-th edge connects nodes $a_i$ and $b_i$.

For each test case, output a single integer in a line indicating the answer.

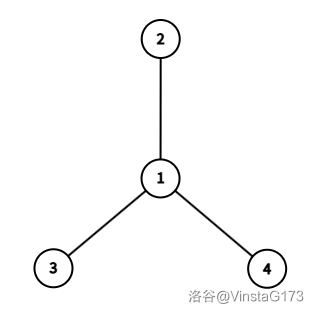
**【Sample 1 Explanation】** The structure of the tree is shown in the figure below.  Let $(u, v)$ denote that Little Y's piece is at $u$ and Little S's piece is at $v$. For the first test case, the following counted movement schemes cause Little Y's piece to pass through $1$ and Little S's piece to pass through $3$: ::cute-table{tuack} | Scheme ID | Movement Sequence | Scheme ID | Movement Sequence | | :-: | :-: | :-: | :-: | | $1$ | $(2,1)\to(1,3)$ | $2$ | $(1,3)\to(2,1)$ | | $3$ | $(4,1)\to(1,3)$ | $4$ | $(1,3)\to(4,1)$ | | $5$ | $(1,1)\to(3,3)$ | $6$ | $(3,3)\to(1,1)$ | | $7$ | $(2,2)\to(1,1)\to(3,3)$ | $8$ | $(3,3)\to(1,1)\to(2,2)$ | | $9$ | $(4,4)\to(1,1)\to(3,3)$ | $10$ | $(3,3)\to(1,1)\to(4,4)$ | | $11$ | $(1,3)\to(3,1)$ | $12$ | $(3,1)\to(1,3)$ | | $13$ | $(1,3)$ | Total: $13$ schemes. For the second test case, the following counted movement schemes cause Little Y's piece to pass through $2$ and Little S's piece to pass through $3$: ::cute-table{tuack} | Scheme ID | Movement Sequence | Scheme ID | Movement Sequence | | :-: | :-: | :-: | :-: | | $1$ | $(2,2)\to(1,1)\to(3,3)$ | $2$ | $(3,3)\to(1,1)\to(2,2)$ | | $3$ | $(2,1)\to(1,3)$ | $4$ | $(1,3)\to(2,1)$ | | $5$ | $(2,3)$ | Total: $5$ schemes. **【Sample 2】** See counting2.in and counting2.ans in the problem attachment. This sample satisfies the special properties of test data 1. **【Sample 3】** See counting3.in and counting3.ans in the problem attachment. This sample satisfies special property A. **【Sample 4】** See counting4.in and counting4.ans in the problem attachment. This sample satisfies special property B, where the first two test cases satisfy $n \le 10^3$. **【Sample 5】** See counting5.in and counting5.ans in the problem attachment. This sample satisfies special property C, where the first two test cases satisfy $n \le 10^3$. **【Data Range】** For all test data, it is guaranteed: + $1 \le T \le 5$; + $1 \le y, s, a_i, b_i \le n \le 10^5$; + $y \neq s$. ::cute-table{tuack} | Test Data ID | $n \le$ | Special Property | Test Data ID | $n \le$ | Special Property | | :-: | :-: | :-: | :-: | :-: | :-: | | $1\sim3$ | $100$ | None | $11\sim13$ | $10^5$ | A | | $4\sim5$ | $10^3$ | B | $14\sim15$ | ^ | B | | $6\sim7$ | ^ | C | $16\sim17$ | ^ | C | | $8\sim10$ | ^ | None | $18\sim20$ | ^ | None | Special Property A: The tree is a complete binary tree, i.e., for $i \ge 2$, node $i$ is connected to node $\lfloor \frac{i}{2} \rfloor$. Special Property B: The tree is a star graph, i.e., there exists one node connected to all other nodes. Special Property C: The tree is a path, i.e., the degree of every node does not exceed $2$.