P14263 [ROI 2015 Day1] 纪念碑

**译自 [ROI 2015](https://neerc.ifmo.ru/school/archive/2014-2015.html) Day1 T2.** ***[Памятник](https://neerc.ifmo.ru/school/archive/2014-2015/ru-olymp-roi-2015-day1.pdf)***

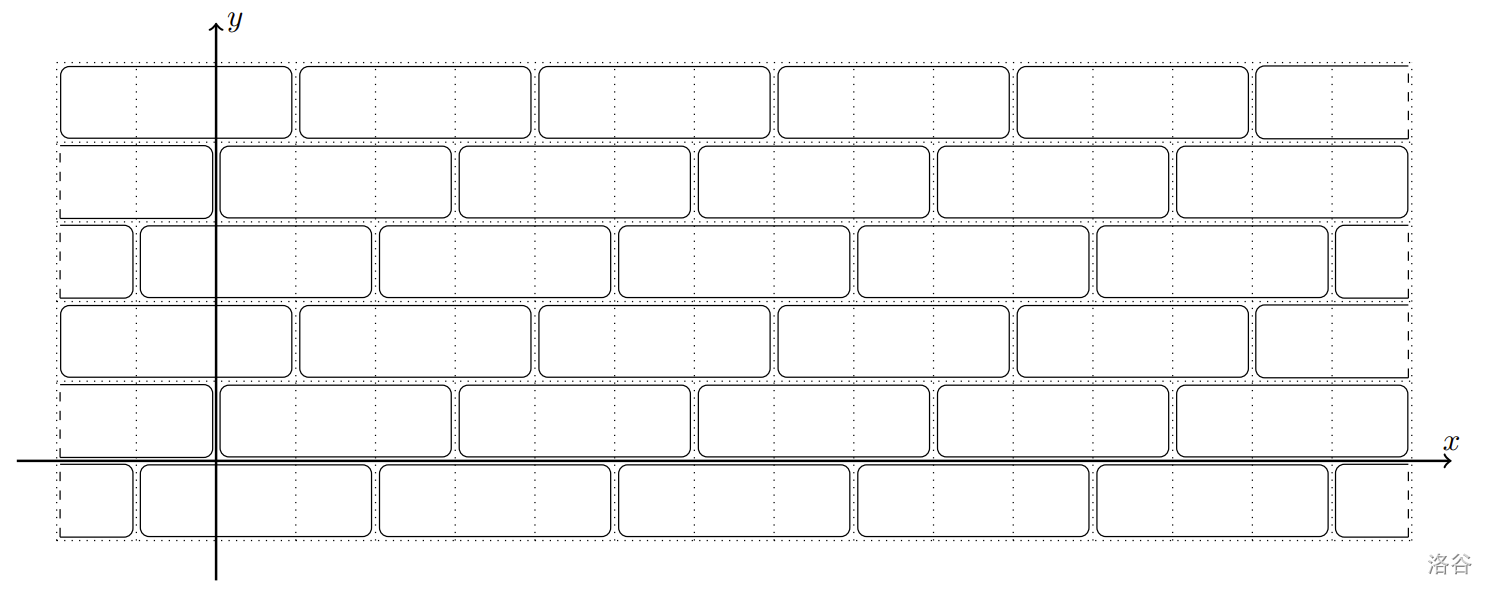
阿尔汉格尔斯克市中心的一处广场铺设着大小为 $1 \times k$ 的长方形地砖。若建立一个坐标系，使其中一块地砖的左下角位于坐标点 $(0, 0)$，则所有地砖的左下角坐标可表示为 $(i \cdot k + j,\, j)$，其中 $i$ 和 $j$ 为任意整数。 :::align{center}  ::: 现在在广场上计划建立一座纪念碑，以纪念著名的阿尔汉格尔斯克作家兼画家斯捷潘·皮萨霍夫。为了安装纪念碑，需要移除所有**完全或部分**位于其基座下方的地砖。 纪念碑的基座是一个顶点坐标为整数的多边形，其所有边都**平行于坐标轴**。已知任意一条平行于坐标轴的直线与该多边形相交时，最多只会形成一个连续的线段。 在选择纪念碑的放置位置时，只允许**平移**该多边形（即沿平行于坐标轴的方向移动），而不能旋转或缩放。目标是找到一种放置方式，使得需要移除的地砖数量最少。 请编写一个程序，计算安装纪念碑时**最少需要移除的地砖数量**。

第一行包含两个整数 $n$ 和 $k$，分别表示纪念碑基座的顶点数以及每块地砖的边长。 接下来的 $n$ 行中，每行包含两个整数 $x_i$ 和 $y_i$，表示基座第 $i$ 个顶点的坐标。顶点按照**逆时针顺序**给出。

输出一个整数——纪念碑可以放置的情况下，需要移除的地砖的最小数量。

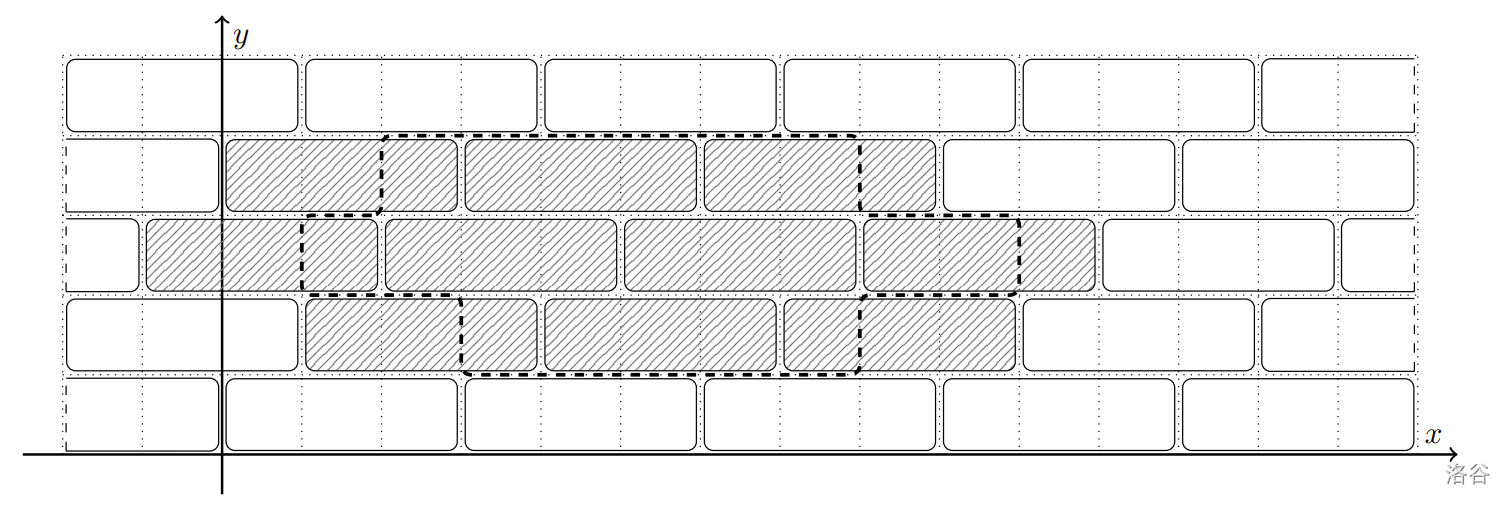
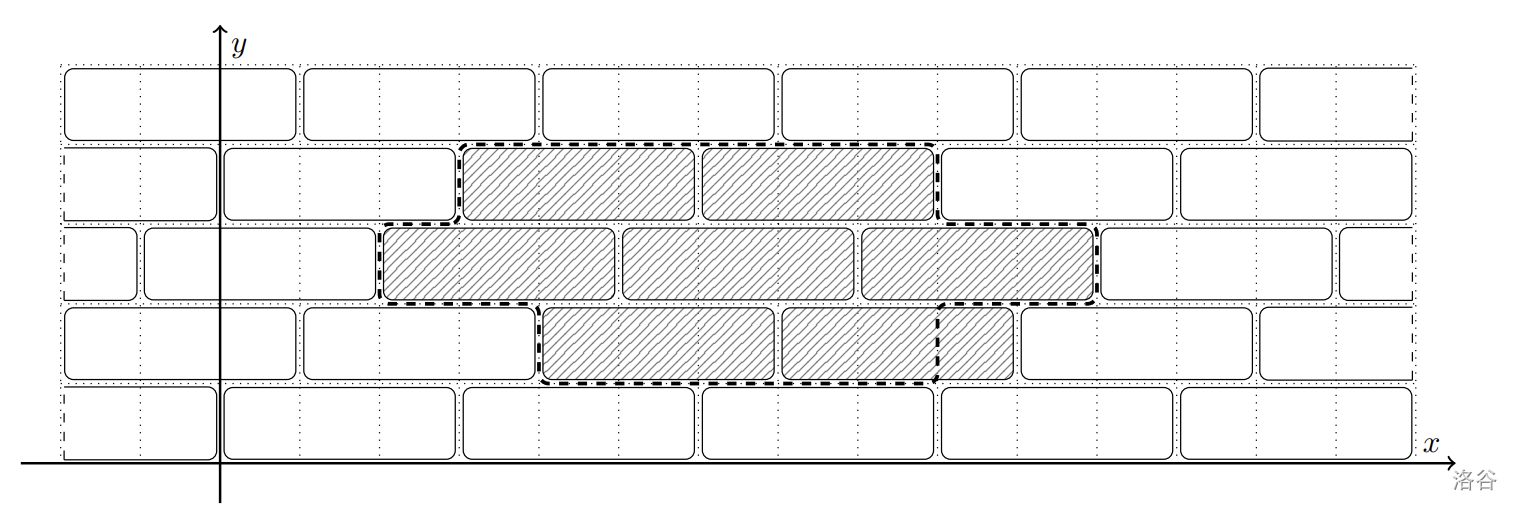
### 样例解释 下图展示了第一个样例中纪念碑基座的**初始位置**。 :::align{center}  ::: 随后展示了第一个样例中纪念碑基座的**最优放置位置**，此时需要移除的地砖数量最少。 :::align{center}  ::: ### 数据范围 | 子任务编号 | 分值 | $n$ | $k$ | $x_i, y_i$ 的范围 | |:--:|:--:|:--:|:--:|:--:| | 1 | 32 | $1 \le n \le 50$ | $1 \le k \le 50$ | $0 \le x_i, y_i \le 50$ | | 2 | 37 | $1 \le n \le 1000$ | $1 \le k \le 1000$ | $0 \le x_i, y_i \le 1000$ | | 3 | 31 | $1 \le n \le 100\,000$ | $1 \le k \le 100\,000$ | $0 \le x_i, y_i \le 1\,000\,000$ |