P14269 [ROI 2015 Day2] 警报系统

**译自 [ROI 2015](https://neerc.ifmo.ru/school/archive/2014-2015.html) Day2 T4.** ***[Сигнализация](https://neerc.ifmo.ru/school/archive/2014-2015/ru-olymp-roi-2015-day2.pdf)***

一个地下掩体由 $n$ 个房间组成，这些房间通过 $n - 1$ 条走廊相连。每条走廊连接两间不同的房间，并具有一定的长度。掩体的结构保证了从任意一个房间 $i$ 都可以到达另一个房间 $j$。注意，存在且仅存在一条路径，使得在该路径中没有任何走廊被重复经过。由这些走廊长度的总和定义为房间 $i$ 与房间 $j$ 之间的**距离**，记作 $\rho(i, j)$。 每个房间都装有一套声响警报系统，由警报器（喇叭）和声波感应器组成。当房间 $i$ 的警报器被启动时，它会激活所有与其距离不超过 $d_i$ 的房间的声波感应器，其中 $d_i$ 表示该警报器的有效传播半径。换句话说，如果房间 $i$ 的警报器被启动，那么所有满足 $\rho(i, j) \le d_i$ 的房间 $j$ 的警报器也会被自动启动。这些被自动启动的警报器反过来又可能触发更多的警报器，以此类推。 在紧急情况下，需要人工启动一部分警报器。这些被人工启动的警报器会自动触发其他警报器，最终应当使得所有房间的警报器都被启动。安全规范要求必须选择一个**最小的人工启动警报器集合**，以确保最终所有房间的警报器都会被启动。 请编写一个程序，计算满足安全规范所需的**最少人工启动警报器数量**。

第一行包含一个整数 $n$ —— 房间的数量。 第二行包含 $n$ 个整数 $d_i$，第 $i$ 个整数表示位于第 $i$ 间房间的警报器的最大传播距离（$0 \le d_i \le 10^9$）。 接下来的 $n - 1$ 行描述了掩体内的走廊。第 $i$ 行包含三个整数 $u_i$, $v_i$, $l_i$，其中 $u_i$ 和 $v_i$ 是被走廊连接的两个不同房间编号，$l_i$ 表示该走廊的长度（$1 \le u_i, v_i \le n$；$1 \le l_i \le 10^9$）。

输出一个整数 —— 表示必须人工启动的警报器的最小数量。

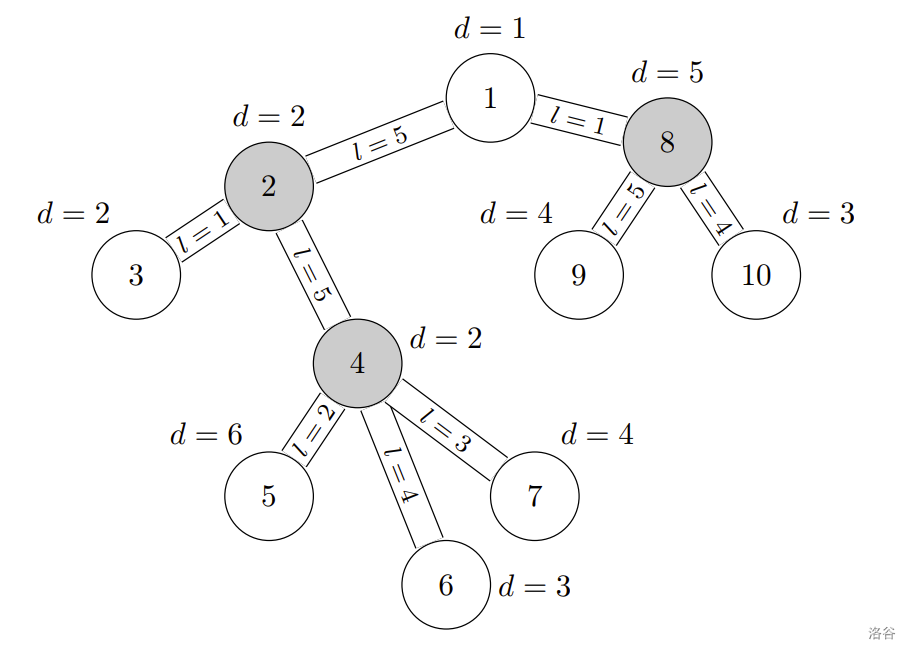
### 样例解释 在样例测试中： - 房间 4 的警报器会激活房间 5 的警报器，房间 5 的警报器又会激活房间 6 和房间 7 的警报器； - 房间 2 的警报器会激活房间 3 的警报器； - 房间 8 的警报器会激活房间 1、9 和 10 的警报器。 :::align{center}  ::: ### 数据范围 | 子任务编号 | 分值 | $n$ 的范围 | |:--:|:--:|:--:| | 1 | 16 | $1 \le n \le 15$ | | 2 | 23 | $1 \le n \le 100$ | | 3 | 17 | $1 \le n \le 3000$ | | 4 | 24 | $1 \le n \le 100\,000$ | | 5 | 20 | $1 \le n \le 300\,000$ |