P14272 [ROI 2014 Day1] 玩具自动售货机

**译自 [ROI 2014](https://neerc.ifmo.ru/school/archive/2013-2014.html) Day1 T1.** ***[Автомат с игрушками](https://neerc.ifmo.ru/school/archive/2013-2014/ru-olymp-roi-2014-statement-day1.pdf)***

在 E 城的娱乐中心安装了一台新一代的游戏自动机。玩家可以向机器中投入硬币，并观察硬币从上到下穿过一个分叉的管道迷宫。 迷宫中共有 $n$ 个节点，编号从 $1$ 到 $n$。每次投入硬币时，硬币会首先进入第 $1$ 个节点。除第一个节点外，每个节点都恰好有一条从上方通入的管道，硬币可沿着这条管道进入该节点。从每个节点出发，最多有两条向下延伸的管道：一条通向左侧，一条通向右侧。 每条管道都有一定的**宽度**。当硬币到达某个节点时，它会沿着**更宽**的管道向下滑落；若两条管道宽度相同，则硬币选择**左边**的管道。 当硬币通过某条管道后，该管道的宽度会减少 $1$。宽度为 $0$ 的管道无法再通过硬币。如果硬币到达某个节点，而该节点已无可通行的管道，则机器停止运作，等待下一枚硬币投入。 最初，每个节点中都放有一个玩具。当硬币**第一次**到达某个节点时，该节点中的玩具会被送给投入该硬币的玩家。 潘克拉特非常喜欢编号为 $v$ 的节点中的玩具。请编写一个程序，确定潘克拉特最少需要投入多少枚硬币，才能获得节点 $v$ 中的玩具。

第一行包含一个整数 $n$ —— 迷宫中的节点数量。 接下来的 $n$ 行依次描述所有节点。第 $k$ 行描述编号为 $k$ 的节点，包含四个整数 $a_k$, $u_k$, $b_k$, $w_k$： 若节点 $k$ 有一条**左管道**，则： - $a_k$ 表示该管道通向的节点编号（满足 $k < a_k \le n$）； - $u_k$ 表示该管道的初始宽度； 若节点 $k$ 没有左管道，则 $a_k = u_k = 0$。 同理，若节点 $k$ 有一条**右管道**，则： - $b_k$ 表示该管道通向的节点编号（满足 $k < b_k \le n$）； - $w_k$ 表示该管道的初始宽度； 若节点 $k$ 没有右管道，则 $b_k = w_k = 0$。 最后一行包含一个整数 $v$（$1 \le v \le n$）—— 潘克拉特想要的玩具所在节点编号。 保证除第一个节点外，每个节点都有且仅有一条进入它的管道。

输出一个整数 —— 潘克拉特需要投入的最少硬币数量，才能获得编号为 $v$ 的节点中的玩具。如果无法获得该玩具，则输出 $-1$。

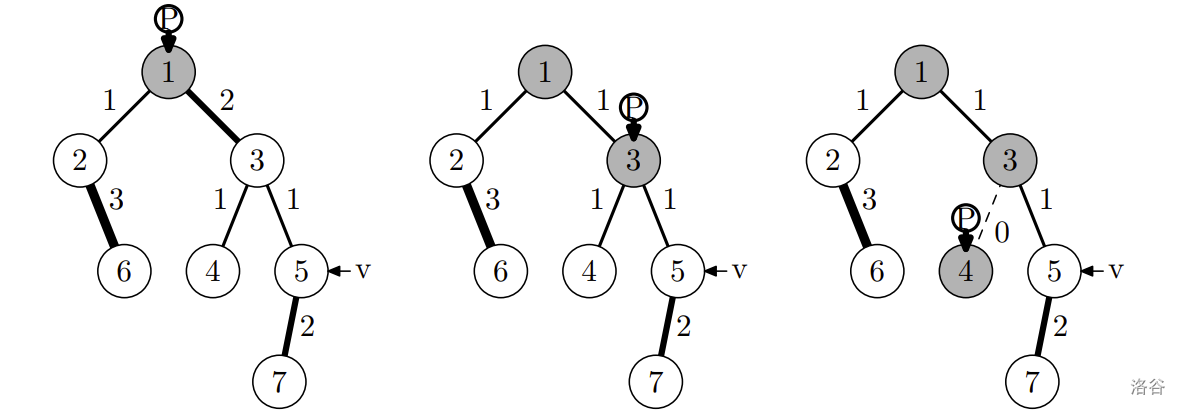
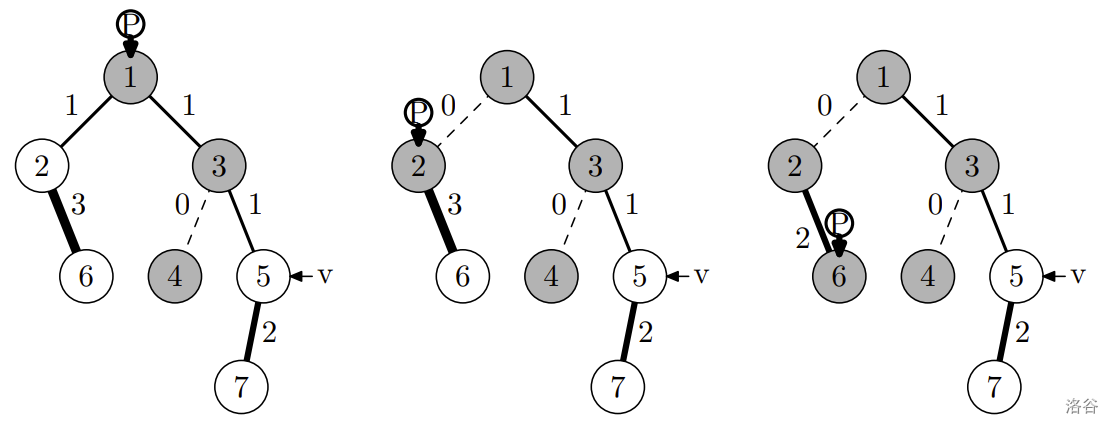
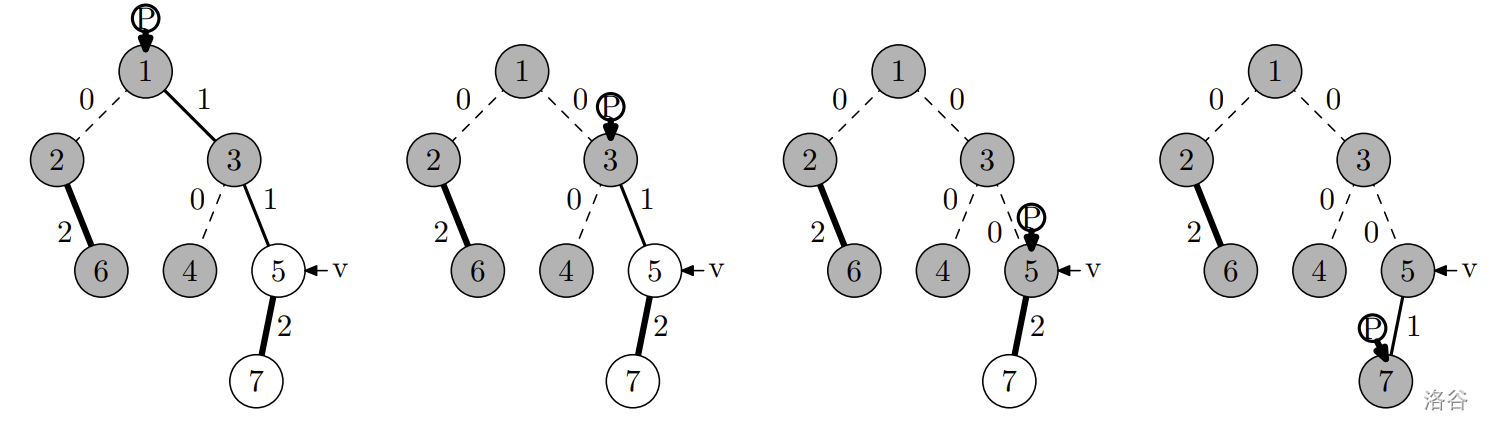
### 样例解释 在第一个样例中： - 第一枚硬币经过的路径如下，玩家获得编号为 1、3 和 4 的节点中的玩具： :::align{center}  ::: - 第二枚硬币经过的路径如下，玩家获得编号为 2 和 6 的节点中的玩具： :::align{center}  ::: - 第三枚硬币经过的路径如下，玩家获得编号为 5 和 7 的节点中的玩具： :::align{center}  ::: ### 数据范围 本题包含两个子任务。每个子任务使用独立的测试集进行评测，只有当某个子任务的所有测试通过时，才能获得对应分数。 ### 子任务 1 - $1 \le n \le 100$ - $1 \le u_k, w_k \le 300$ - 分值：50 分 ### 子任务 2 - $1 \le n \le 10^5$ - $1 \le u_k, w_k \le 10^9$ - 分值：50 分